并查集是大二时候学的,没想到还能 Get 新使用姿势。本周新活,讲一下使用并查集模拟数组中元素的删除,特定情境下可以代替链表或二叉搜索树!附带 JavaScript 风味的前三题。
「难以删除」
我们先来考虑一个抽象的问题:给定一个数组 A,要求实现两种操作:
- 查询
A中大于等于某个给定值x的最小元素 - 删除
A中大于等于某个给定值x的最小元素
想要使用简单数据结构实现这两种操作是很困难的。第一个操作很简单,只需要把 A 预先排序,然后二分搜索即可以 O(log N) 的速度实现查询。但如果将 A 放置在一个数组中,就不能方便的实现删除操作,数组元素的删除操作时间复杂度是 O(N), 效率低下。
一般来说,能够实现这两种操作的数据结构是二叉搜索树,C++ 中的 set 或者 map 以及 Java 中的 TreeMap 一般就采用二叉搜索树(如红黑树)实现,能够以 O(log N) 速度实现查询和删除操作。但二叉搜索树有一些问题,
- 尽管这两种容器时间复杂度名义上是
O(log N), 但实际上是比较慢的,因为二叉树是一种较为复杂的数据结构,还存在动态内存申请 - 并不是所有的语言都有内置的二叉搜索树实现,以及,由于过于复杂,想要自行实现这类数据结构是非常困难的
这个需求中的痛点就在于删除。数组中尽管不能高效的实现删除,但有种折中办法,标记删除,也被形象的称之为「墓碑」。就是不实际删除某个元素,而是做一个删除标记(墓碑)。但如果数组中大量的元素都被删除,留下来了大量墓碑,就会影响查找效率。想象一个大部分元素都是墓碑的数组,如果我们想要查找某个大于等于某个值的最小元素,运行二分法查找到满足要求的元素后,如果这个元素不幸是个墓碑,就得向后逐个检索,寻找第一个不是墓碑的元素,这个操作最坏就会导致时间复杂度变成 O(N).
// 例子
// 一个有序数组初始状态,
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
// 标记删除 3, 4, 6, 7
[0, 1, 2, x, x, 5, x, x, 8, 9]
// 此时查询大于等于 3 的第一个元素,会查询到一个墓碑
[0, 1, 2, x, x, 5, x, x, 8, 9]
^
// 之后需要后移两次,才能找到第一个有效的元素 5
[0, 1, 2, x, x, 5, x, x, 8, 9]
-> -> ^
最大元素并查集
那么,有没有办法快速找到任意一个位置之后第一个不是墓碑的元素的?可以使用一种特殊的并查集实现。我们知道,一般的并查集建立在从 0 开始的连续自然数数组上,初始化时这些数字各自在一个集合中。之后可以通过归并操作将集合合并,此时查询某个数字的集合序号会返回集合中某个元素作为集合序号(这个元素在没有新的归并操作前对整个集合是固定的)。并查集内部实现为一种树状结构,返回的这个元素其实就是树的根节点。
// 一个正常的并查集
struct MergeFindSet {
std::vector<int> p;
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
void merge(int root, int child) { p[find(child)] = find(root); }
MergeFindSet(int n) : p(n) {
for (int i = 0; i < n; i++) p[i] = i;
}
};
这里实现一个特殊版本的并查集,这个实现总是会返回集合中最大的元素。
// 一个特殊的并查集,总是返回集合中最大元素
struct MergeBigger {
std::vector<int> p;
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
void merge(int x, int y) {
// 进行归并操作时,总是指向较大的元素作为新的集合根节点
int rx = find(x), ry = find(y);
p[std::min(rx, ry)] = std::max(rx, ry);
}
MergeBigger(int n) : p(n) {
for (int i = 0; i < n; i++) p[i] = i;
}
};
并查集实现数组元素删除
并查集的结构其实跟单链表有相似之处。在数组删除问题中,我们可以使用并查集的根节点来指代「下一个有效元素」。
vector<int> nums = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
MergeBigger me(10);
// 标记删除元素 3, 将并查集中 3 指向 4
me.merge(3, 4);
// 标记删除 4
me.merge(4, 5);
// 标记删除 x 也即:
// me.merge(x, x + 1);
// 查询大于等于 3 的第一个有效元素
me.find(3); // return: 5
上一周的周四第四题就可以使用该技巧加速 BFS, 要比评论区中大部分使用二叉搜索树的解法更快。本周第四题也可以如法炮制,使用该技巧「删除」BFS 访问过的格点。

struct MergeBigger {
std::vector<int> p;
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
void merge(int x, int y) {
int rx = find(x), ry = find(y);
p[std::min(rx, ry)] = std::max(rx, ry);
}
MergeBigger(int n) : p(n) {
for (int i = 0; i < n; i++) p[i] = i;
}
};
class Solution {
public:
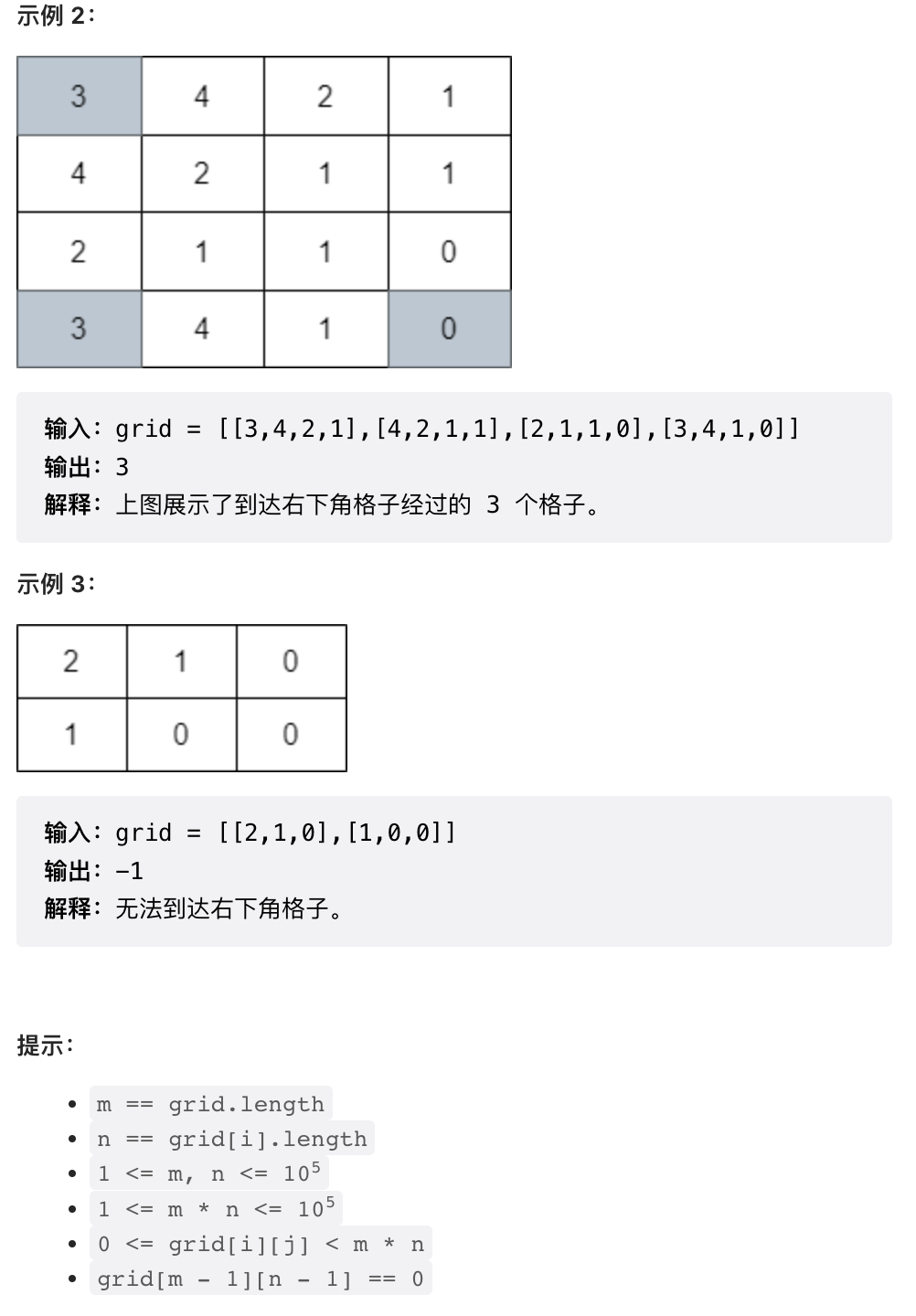
int minimumVisitedCells(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<MergeBigger> jump1(m, MergeBigger(n + 1)), jump2(n, MergeBigger(m + 1));
vector<vector<int>> dp(m, vector<int>(n, -1));
queue<pair<int, int>> q;
auto visit = [&](int i, int j, int step) {
jump1[i].merge(j, j + 1);
jump2[j].merge(i, i + 1);
dp[i][j] = step;
q.push({i, j});
};
visit(0, 0, 1);
while(q.size()) {
int i = q.front().first, j = q.front().second;
q.pop();
int dist = grid[i][j], step = dp[i][j] + 1;
for(int x = jump2[j].find(i); x <= i + dist and x < m; x = jump2[j].find(x)) {
visit(x, j, step);
}
for(int y = jump1[i].find(j); y <= j + dist and y < n; y = jump1[i].find(y)) {
visit(i, y, step);
}
}
return dp[m - 1][n - 1];
}
};
最后,本周周赛前三题无甚可说,但我尝试了一下使用 JavaScript 写算法题,那是相当的别扭,不推荐。
1.

/**
* @param {number[][]} nums
* @return {number}
*/
var diagonalPrime = function(nums) {
function isPrime(x) {
for(let i = 2; i * i <= x; i++) {
if(x % i == 0) {
return false;
}
}
return x >= 2;
}
let res = 0;
const n = nums.length;
for(let i = 0; i < n; i++) {
const x = nums[i][i], y = nums[i][n - 1 - i];
if(isPrime(x)) {
res = Math.max(x, res);
}
if(isPrime(y)) {
res = Math.max(y, res);
}
}
return res;
};
2.

/**
* @param {number[]} nums
* @return {number[]}
*/
var distance = function(nums) {
const n = nums.length;
const idx = new Map();
for(let i = 0; i < n; i++) {
if(!idx.has(nums[i])) {
idx.set(nums[i], [])
}
idx.get(nums[i]).push(i);
}
let arr = new Array(n).fill(0);
for(const pos of idx.values()) {
const m = pos.length;
let pre = 0;
for(let j = 0; j < m; j++) {
arr[pos[j]] += pos[j] * j - pre;
pre += pos[j];
}
let suf = 0;
for(let j = m - 1; j >= 0; j--) {
arr[pos[j]] += suf - pos[j] * (m - 1 - j);
suf += pos[j];
}
}
return arr;
};
3.

这个题目我涨了见识了,JavaScript 的排序默认是字典序,[1, 2, 10] 排序后是 [1, 10, 2] 必须要加上一个比较函数才能正常排序。
/**
* @param {number[]} nums
* @param {number} p
* @return {number}
*/
var minimizeMax = function(nums, p) {
nums.sort((x, y) => x - y);
const n = nums.length;
function countPairs(nums, dist) {
let res = 0;
for(let i = 0; i + 1 < n;) {
if(nums[i + 1] - nums[i] <= dist) {
res += 1;
i += 2;
} else {
i++;
}
}
return res;
}
let left = 0, right = nums[n - 1];
while(left < right) {
const mid = Math.floor((left + right) / 2);
const pairs = countPairs(nums, mid);
if(pairs >= p) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
};