本周沉迷 ChatGPT, 周赛也没心情打了。整个活,使用 ChatGPT 打周赛效果如何?在我的协助下 ChatGPT 过掉了 2 题,在 22308 名选手中排名 3242,超越 85% 人类选手。程序员饭碗不保!
跟我走,与 AI 并肩作战,体会 AI 是如何思考的!
1.

这个题目比较适合 ChatGPT 因为题干简短,描述清晰。我将英文题干发给 ChatGPT-4,
write python code to solve this problem,
There is a bag that consists of items, each item has a number 1, 0, or -1 written on it.
You are given four non-negative integers numOnes, numZeros, numNegOnes, and k.
The bag initially contains:
numOnes items with 1s written on them.
numZeroes items with 0s written on them.
numNegOnes items with -1s written on them.
We want to pick exactly k items among the available items. Return the maximum possible sum of numbers written on the items.
令人震惊的是,ChatGPT 出色的解决了这个问题:
# ChatGPT
class Solution:
def kItemsWithMaximumSum(self, numOnes: int, numZeros: int, numNegOnes: int, k: int) -> int:
total_items = numOnes + numZeros + numNegOnes
# If the number of items to pick is more than the total items, return None
if k > total_items:
return None
# Calculate the maximum possible sum
max_sum = min(k, numOnes) # Pick as many 1s as possible, up to k
# Calculate remaining items to pick after choosing 1s
remaining_k = k - max_sum
# Pick as many 0s as possible (doesn't affect sum)
remaining_k -= min(remaining_k, numZeros)
# If there are still items to pick, pick -1s and update the sum
if remaining_k > 0:
max_sum -= remaining_k
return max_sum
当然本题甚为简单,过掉并不惊讶。
我对 ChatGPT 不服,你看它啰哩啰嗦一大堆,我一行就行了。
# Jiahao
class Solution:
def kItemsWithMaximumSum(self, numOnes: int, numZeros: int, numNegOnes: int, k: int) -> int:
return k if numOnes >= k else numOnes if numOnes + numZeros >= k else numOnes - (k - numOnes - numZeros)
3.
我们跳过第二题,因为 AI 没做出来。先看第三题,

我们先来看看题目本身。为了理解 AI 的思路,读者至少要明白这道题目在做什么。
考虑对于某次 Query, 大于 Query 的数字集合为 A,小于 Query 的数字集合为 B 要求的操作次数就等于 sum(A) - Query * len(A) + Query * len(B) - sum(B). 具体实现,这道题目最优解是双指针方法。可以在 O(M+N) 时间内求解。
我们可以先把数字和 Query 排序,然后使用双指针做一次遍历即可。
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
m, n= len(queries), len(nums)
nums.sort()
qs = sorted((x, i) for i, x in enumerate(queries))
total = sum(nums)
j = pre = 0
res = [0] * m
for x, i in qs:
while j < n and nums[j] <= x:
pre += nums[j]
j += 1
res[i] = (x * j - pre) + (total - pre - x * (n - j))
return res
除了双指针之外,二分法也是可以解决问题的。二分法基本思路是,也先把 nums 排序,然后对每个 Query 利用二分法找到大于 Query 的所有数字和小于 Query 的所有数字,然后分别求和就可以了。可以使用前缀和加速求和过程。
同样的,我们把题目发给 ChatGPT,
# ChatGPT
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
answer = []
total_sum = sum(nums)
n = len(nums)
for query in queries:
diff_sum = 0
for num in nums:
diff_sum += abs(num - query)
answer.append(diff_sum)
return answer
ChatGPT 出色的回答了这个问题,它的这份代码逻辑是对的!但是会超时。我并没有把数据规模发给它,超时可以理解。我发出指令 you get TLE. make the code faster. ChatGPT 的表现非常令人惊讶,它正确理解了我的意思,然后试图使用二分搜索加速。
# Jiahao: you get TLE. make the code faster
# ChatGPT
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
answer = []
nums.sort()
def binary_search(nums, target):
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
def calc_operations(nums, idx, target):
operations = 0
for i in range(len(nums)):
operations += abs(nums[i] - target)
return operations
for query in queries:
idx = binary_search(nums, query)
operations = calc_operations(nums, idx, query)
answer.append(operations)
return answer
它这个代码写的头头是道,甚至把我都糊弄过去了,我觉得应该能过,但实际上仍然是个 TLE. 我以为是 Python 太慢了,命令 ChatGPT 用 C++ 重写这段代码(ChatGPT 能够有效进行代码片段的翻译,我在实战中常常使用),仍然 TLE. 我提示它使用双指针,但它错的更离谱了。
我仔细看了一遍它的代码,发现它写了个二分搜索其实是装样子的,压根没用上,它那个二分搜索返回变量 idx 没有使用。我决定再试一下。我指出,go back to the binary search python version. you didn't use the binary search result idx. 令人感动,它听懂了,
def calc_operations(nums, idx, target):
operations = 0
for i in range(idx):
operations += abs(nums[i] - target)
for i in range(idx, len(nums)):
operations += abs(nums[i] - target)
return operations
这个代码就看到曙光了,它只要能分别处理 idx 两侧的求和就行了,我指出,you need to fast up the calculation of operators in the two side of idx, you cannot add them one by one. it's too slow. 它正确理解了我的意思。但它没有使用前缀和进行优化,而是调用了 python 的 sum 函数。我直接给出提示,use a pre-calculated prefix sum array instead of sum function. 它又非常惊艳的正确进行了前缀和计算,并几乎正确的替换了 sum 函数,但不知为啥它把 target 搞丢了,
def calc_operations(nums, idx, target):
operations = 0
operations += nums[idx - 1] * idx - prefix_sum[idx] if idx > 0 else 0
operations += prefix_sum[-1] - prefix_sum[idx] - nums[idx] * (len(nums) - idx) if idx < len(nums) else 0
return operations
我提示 you didn't use variable target in the calc_operations function, you need to use it. 提示之后,它成功解决了这个问题,
def min_operations(nums, queries):
answer = []
nums.sort()
prefix_sum = [0] * (len(nums) + 1)
for i in range(len(nums)):
prefix_sum[i + 1] = prefix_sum[i] + nums[i]
def binary_search(nums, target):
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
def calc_operations(nums, idx, target):
operations = 0
operations += target * idx - prefix_sum[idx] if idx > 0 else 0
operations += prefix_sum[-1] - prefix_sum[idx] - target * (len(nums) - idx) if idx < len(nums) else 0
return operations
for query in queries:
idx = binary_search(nums, query)
operations = calc_operations(nums, idx, query)
answer.append(operations)
return answer
这份代码正确,可以通过!
这一题的求解过程令人印象深刻。ChatGPT 其实真的很像人,它「想到」要用二分搜索,但没有用对,在提示下,它一点点改正,最终成功解决问题。
结论:准备下岗!
总体来说,ChatGPT 的表现非常令我惊讶,它在指导之下解决了两道问题,超越(严格来说,大于等于) 85% 人类选手(不过,今天 LeetCode 服务器挂了几十分钟,所以人类选手表现受到一些影响),特别是求解第三题的过程,那种感觉太像以前我做老师给学生讲题了。或许角色很快就会翻转,我们要做被指导的学生了。
我曾经专门分析过解题的思维过程。我自己的体会是,求解一个数学或者物理或者编程题目的过程可以分为两步,首先「寻求思路」,就像第三题中,二分法、双指针,这些就是「思路」。然后,需要严密的将灵感转换成逻辑步骤,最终构成题解。与 ChatGPT 合作的过程,我感觉它的第一步已经做的有模有样了,换句话说,创新性的一步它反而做得好。第二步严密的逻辑验证,它做的还不是那么好,但也已经非常棒了。
最可怕的是,我觉得这是以很高的标准在要求它。网测对人类选手也很难,因为计算机评分,难以糊弄了事。其他非计算机打分的考试中,特别明显的是证明题,其实人类选手也常常是胡说八道。计算题中,人类选手也常常是能套的上的东西就往上搬,而 ChatGPT 也是这么干的。
我个人怀疑,尽管现在 AI 还没有解决「严密推理」这个难题,但这个问题很可能比「理解自然语言」本身要简单,而一旦 AI 将严密推理能力和自然语言理解能力结合起来,我就饭碗不保了。
结论,完了,准备下岗送快递、送外卖,听从 AI 指挥!
下面是 AI 没写出来的两道问题,有兴趣的同学可以看一看!
2.

这个题目就得动点脑筋了。本题可以贪心的求解。考虑从左到右处理 nums, 则每个数在保证大于其左侧的数的前提下,应该尽可能地小(也即尽可能减去一个比较大的质数)。
至于质数列表,可以使用素数筛算法预计算。素数筛是一个速度非常接近 O(n) 的快速算法。我给出的解法:
// 素数筛模板,不难理解
void prime_flags(std::vector<bool>& flags) {
int lim = int(flags.size());
flags[0] = flags[1] = false;
for (int n = 4; n < lim; n += 2) {
flags[n] = false;
}
for (int n = 3; n * n <= lim; n += 2) {
if (flags[n]) {
for (int t = n * 3; t < lim; t += n << 1) {
flags[t] = false;
}
}
}
}
class Solution {
public:
bool primeSubOperation(vector<int>& nums) {
// 使用素数筛算法生成 1000 以内的素数列表
const int x = 1024;
vector<bool> flags(x, true);
prime_flags(flags);
vector<int> ps = {0};
for(int i = 0; i < x; i++) {
if(flags[i]) {
ps.push_back(i);
}
}
const int n = nums.size(), m = ps.size();
for(int i = 0; i < n; i++) {
bool succ = false;
for(int j = m - 1; j >= 0 and not succ; j--) {
// 从大到小检查所有素数,寻找能够维持递增条件的最大的素数作为减数
// 这里也可以使用二分法,但因为 1000 以内的素数不太多,没必要
if(ps[j] < nums[i] and (i == 0 or nums[i] - ps[j] > nums[i - 1])) {
nums[i] -= ps[j];
succ = true;
}
}
if(not succ) {
return false;
}
}
return true;
}
};
同样的,我将本题英文题干发给 ChatGPT, 它给出解法如下,
# ChatGPT
def is_prime(n: int) -> bool:
if n <= 1:
return False
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return False
return True
def find_largest_prime_less_than(n: int) -> int:
for i in range(n - 1, 1, -1):
if is_prime(i):
return i
return None
class Solution:
def primeSubOperation(self, nums: List[int]) -> bool:
for i in range(len(nums) - 1):
largest_prime = find_largest_prime_less_than(nums[i])
if nums[i] - largest_prime < nums[i + 1]:
nums[i] -= largest_prime
else:
return False
return True
它这个写的其实有点那个意思,但在处理 nums[i] 时,它只保证了 nums[i] 小于后一个数,没有检查 nums[i] 是否大于前一个数。相当于它只向右做了检查,没有向左做检查。我试图给它指出错误,发出指令 you didn't check if nums[i] larger than nums[i - 1]. 它至少挺明白了我指示的是什么位置,但显然它无法理解深层的错误,它改的更离谱了。这个题目到此为止。
class Solution:
def primeSubOperation(self, nums: List[int]) -> bool:
for i in range(1, len(nums)):
if nums[i] <= nums[i - 1]:
largest_prime = find_largest_prime_less_than(nums[i])
if nums[i] - largest_prime > nums[i - 1]:
nums[i] -= largest_prime
else:
return False
return True
4.
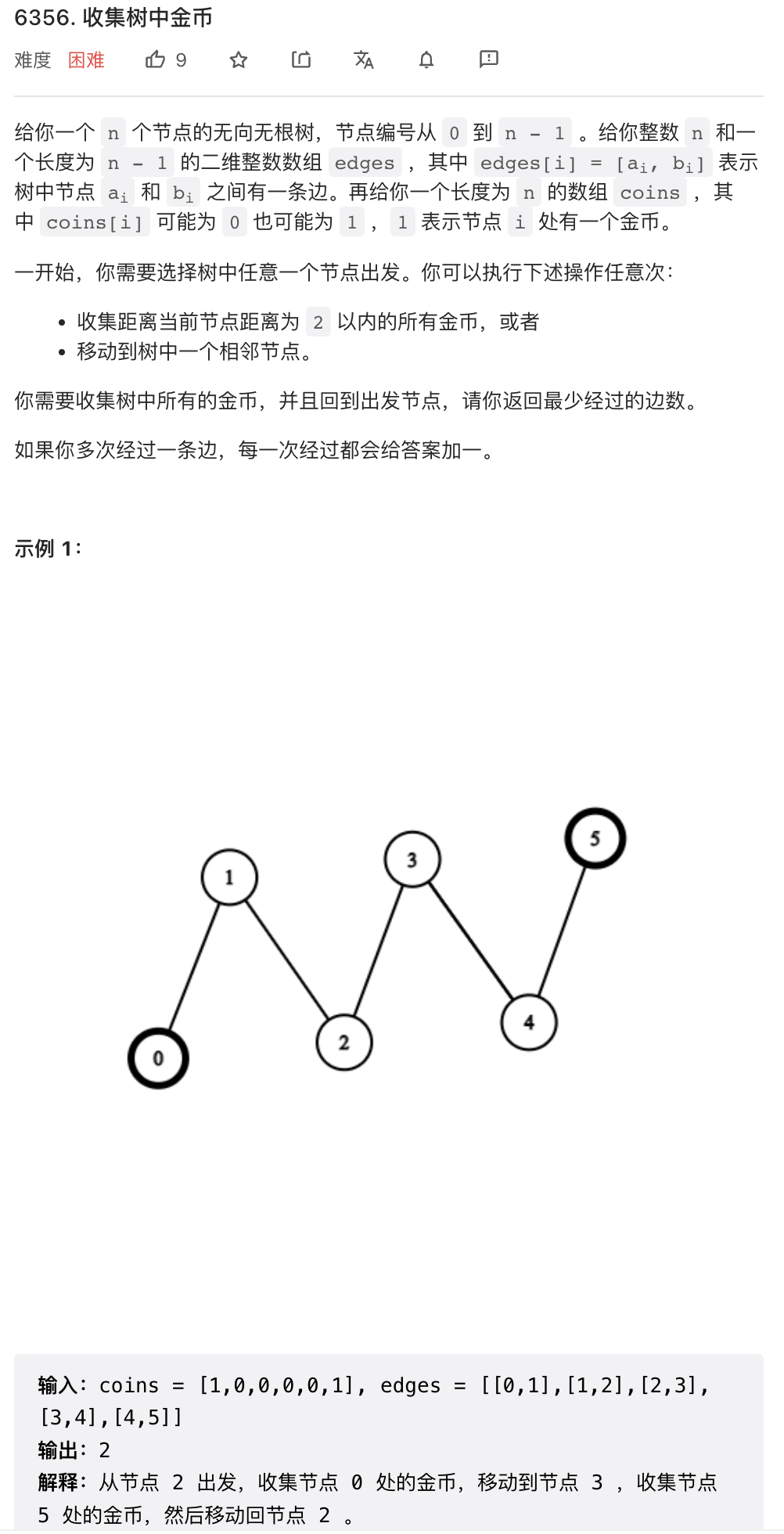
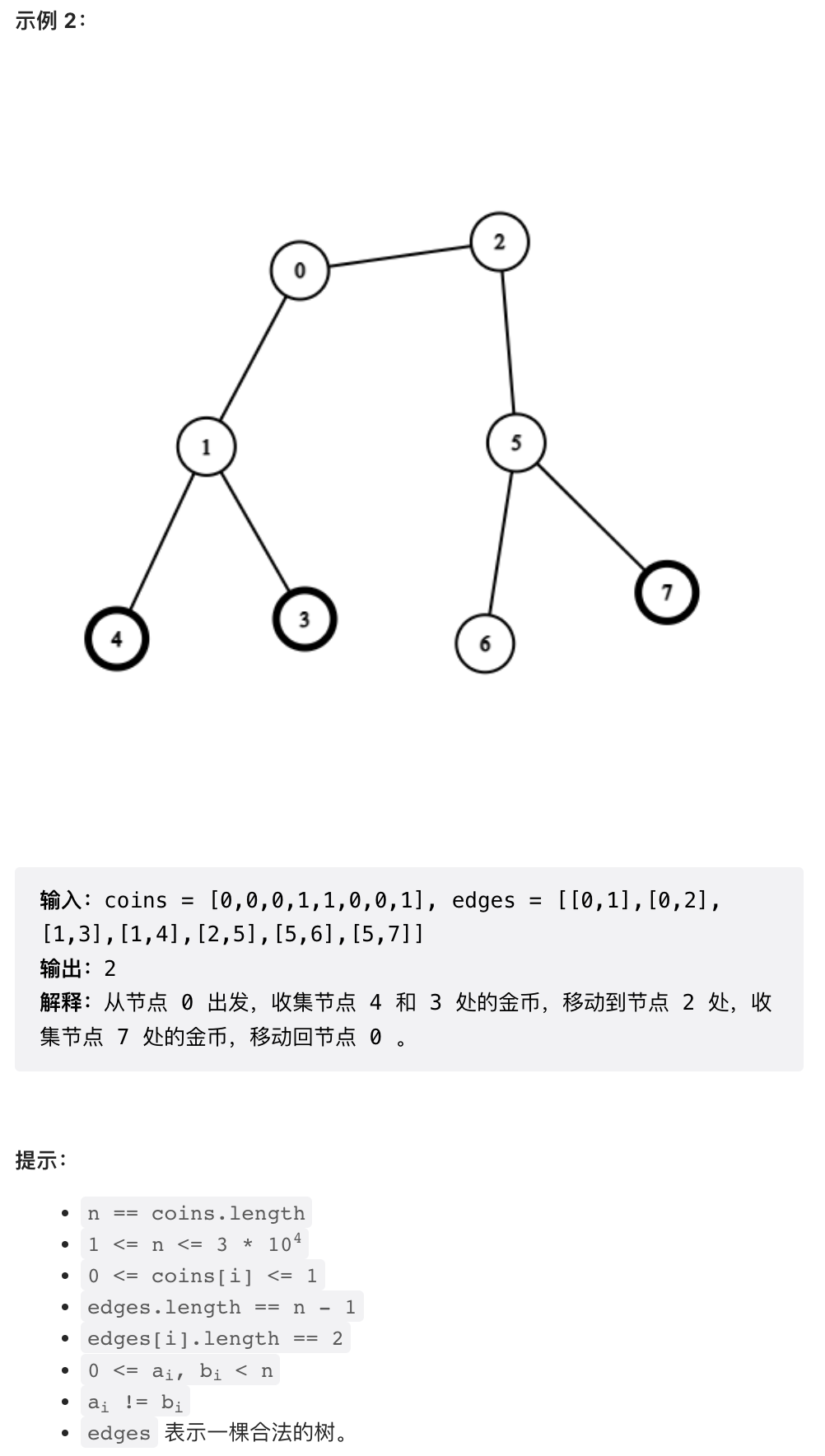
这个问题作为周赛问题,比较复杂。ChatGPT 就不提了,人类选手大部分也是做不出来这道题目的。
求解这个问题,首先需要明白,最终需要遍历的节点是整个树的一个子树。然后需要证明,要便利一个子树并在便利之后回到初始节点,则无论从这棵子树上任何节点出发,需要走的步数都是相通的,而且这个步数等于子树节点数量 (n - 1) * 2. 这个结论不难证明。
这样一来,问题主要难点就是求这棵需要遍历的子树。
在这棵无根树上,我们仍然可以定义叶节点,叶节点就是只跟一个节点相连的结蒂娜。我们可以运行拓扑排序的算法,就是从树的所有叶节点开始删除,删除掉叶节点之后再删除成为叶节点的节点,直到删除整棵树。首先,我们可以把没有硬币的所有叶节点删除掉,这些叶节点一定不会被访问,它们对问题没有影响。然后递归的删除所有按拓扑排序子节点中没有硬币的节点。
然后,剩下的一棵树所有的节点都需要到达,或者到达距离其小于 2 的节点,从而保证这些节点上的硬币被收集。我们可以再运行一遍上述拓扑排序过程,并统计所有高度超过 2 的节点数量,这些节点就是必须要遍历的节点。
这段代码虽然比较长,但实际上拓扑排序重复了两遍,并不十分复杂。
class Solution {
public:
int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {
const int collect_dist = 2;
// 建图,并统计节点度数
int n = coins.size();
vector<vector<int>> g(n);
vector<int> degree(n);
for(auto& e: edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
degree[a]++;
degree[b]++;
}
// 删掉所有没有硬币的子节点,以及整棵子树都没有硬币的节点
// 可以递归的证明,这一步删除之后,剩下的节点都需要收集
// 通过更新 degree 数组来标记哪些节点被删除了
queue<int> q;
for(int i = 0; i < n; i++) {
if(degree[i] == 1 and coins[i] == 0) q.push(i);
}
while(q.size()) {
int i = q.front();
q.pop();
if(!degree[i]) continue;
degree[i] -= 1;
for(int p: g[i]) {
if(!degree[p]) continue;
degree[p] -= 1;
if(degree[p] == 1 and coins[p] == 0) q.push(p);
}
}
// 删除剩下的节点,并统计高度大于 2 的节点个数
// 此时可以保证所有的节点都需要收集,因此不需要检查是否有 coin 了
for(int i = 0; i < n; i++) {
if(degree[i] == 1) q.push(i);
}
vector<int> height(n);
int res = 0;
while(q.size()) {
int i = q.front();
q.pop();
if(!degree[i]) continue;
degree[i] -= 1;
for(int p: g[i]) {
if(!degree[p]) continue;
degree[p] -= 1;
height[p] = max(height[p], height[i] + 1);
if(degree[p] == 1) q.push(p);
}
res += int(height[i] >= 2) * 2;
}
return res;
}
};
我还是试了一下 ChatGPT, 它写了个 DFS 树遍历,我完全看不懂它在干啥反正它不是在做这道题目。我的指导无从下手,放弃。
# ChatGPT
class Solution:
def collectTheCoins(self, coins: List[int], edges: List[List[int]]) -> int:
from collections import defaultdict
def dfs(node, parent):
nonlocal res
cur_coins = coins[node]
max_edge_dist = 0
second_max_edge_dist = 0
for neighbor in tree[node]:
if neighbor != parent:
dist, collected = dfs(neighbor, node)
cur_coins += collected
edge_dist = dist + 1
if edge_dist > max_edge_dist:
second_max_edge_dist = max_edge_dist
max_edge_dist = edge_dist
elif edge_dist > second_max_edge_dist:
second_max_edge_dist = edge_dist
if cur_coins > 0:
res += 2 * (max_edge_dist + second_max_edge_dist)
return max_edge_dist, cur_coins
tree = defaultdict(list)
for a, b in edges:
tree[a].append(b)
tree[b].append(a)
res = 0
dfs(0, -1)
return res