上周周赛非常有意思,但因为有事没有写题解,今天补上简单版。
1.

第一题就非常有意思,这个模拟操作虽然不会超时但太麻烦了。仔细想想,第一次一定会把 n - 1 放上去,第二次一定会把 n - 2 放上去,因此最终一定会把 [2, n] 都放上去。特例是 n = 1 此时第一轮把 n 放上去之后就结束了。因此在 n = 1 时结果是 1 其他情况结果是 n - 1.
class Solution:
def distinctIntegers(self, n: int) -> int:
return max(n - 1, 1)
2.
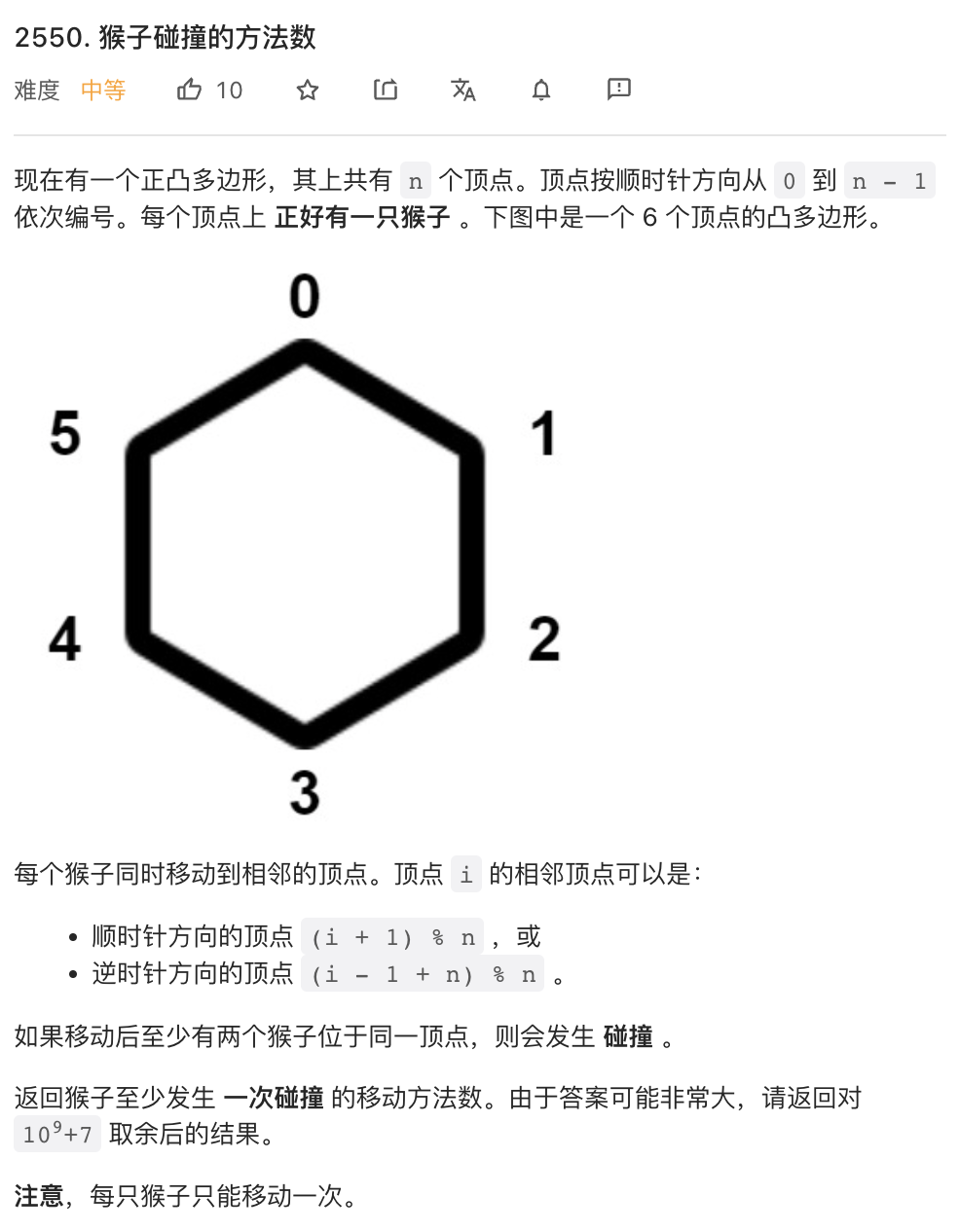

这个题目有点脑筋急转弯:实际上,除了所有的猴子都往同一个方向运动之外的所有情况,都会碰撞。所以不会碰撞的情况总共只有 2 种。总方案有 2^n 种,python 的 pow 函数可以求 2^n % m.
class Solution:
def monkeyMove(self, n: int) -> int:
m = 10 ** 9 + 7
return (pow(2, n, m) - 2 + m) % m
3.

这个题目看似有点像背包问题,但实际上跟动态规划完全没有关系:总的 cost 其实就是首尾两个元素和再加上选取 n - 1 个切分点的 cost. 而切分点可以先枚举所有切分点 cost, 然后做个排序就可以方便的取 MIN N OR MAX N 了。
class Solution:
def putMarbles(self, weights: List[int], k: int) -> int:
sp = sorted(weights[i] + weights[i + 1] for i in range(len(weights) - 1))
return sum(sp[-(k-1):]) - sum(sp[:k-1]) if k != 1 else 0
4.

这是一道比较有新意的题目,而且很容易读错题目。它要求计数的不是顺序四个数,而是中间两个数颠倒。
这道题目很容易联想到逆序对,然后容易联想到本题解法跟逆序对是不是有关联,但这个思路走不通,本题跟逆序对没啥关联。
数据规模提醒我们,本题可能是复杂度接近 O(n^2) 解法。很容易有一个思路:枚举四个坐标中的两个,然后计数符合条件的数字。我尝试了枚举 (i,j), (i,k), (i,l) 最终发现枚举 (j,k) 比较可行。
基本思路是,枚举 (j, k) 然后立即就可以判断 nums[j] > nums[k] 是否满足。之后计数 j 前方小于 nums[k] 的数字个数,和 k 后方大于 nums[j] 的数字个数。这里我们使用了 Fenwick Tree 完成计数,也可以使用 DP 预计算这部分计数。
struct Fenwick {
vector<int> tree;
int n;
Fenwick(int size): n(size + 1), tree(size + 2, 0) {}
void clear() {
fill(tree.begin(), tree.end(), 0);
}
void add(int i, int x) {
for(i++; i <= n; i += i & -i) tree[i] += x;
}
long long prefix(int i) {
long long res = 0;
for(i++; i > 0; i-= i & -i) res += tree[i];
return res;
}
};
class Solution {
public:
long long countQuadruplets(vector<int>& nums) {
long long res = 0;
int n = nums.size();
Fenwick pre(n), suf(n);
for(int j = 1; j < n; j++) {
pre.add(nums[j - 1], 1);
suf.clear();
for(int k = n - 2; k > j; k--) {
suf.add(nums[k + 1], 1);
if(nums[j] > nums[k]) {
res += pre.prefix(nums[k]) * (suf.prefix(n) - suf.prefix(nums[j]));
}
}
}
return res;
}
};