1.

class Solution:
def differenceOfSum(self, nums: List[int]) -> int:
return abs(sum(nums) - sum(int(c) for x in nums for c in str(x)))
2.
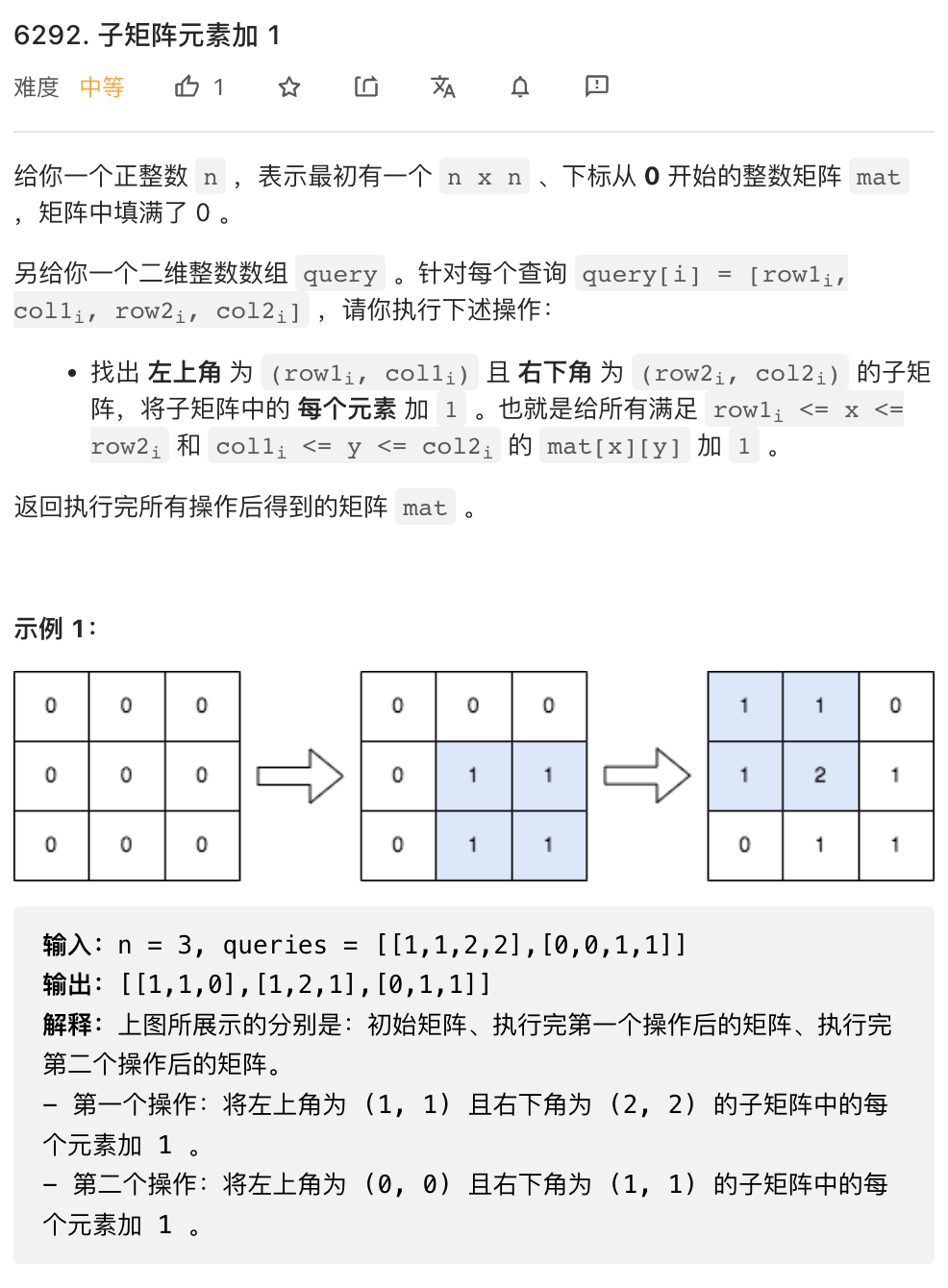
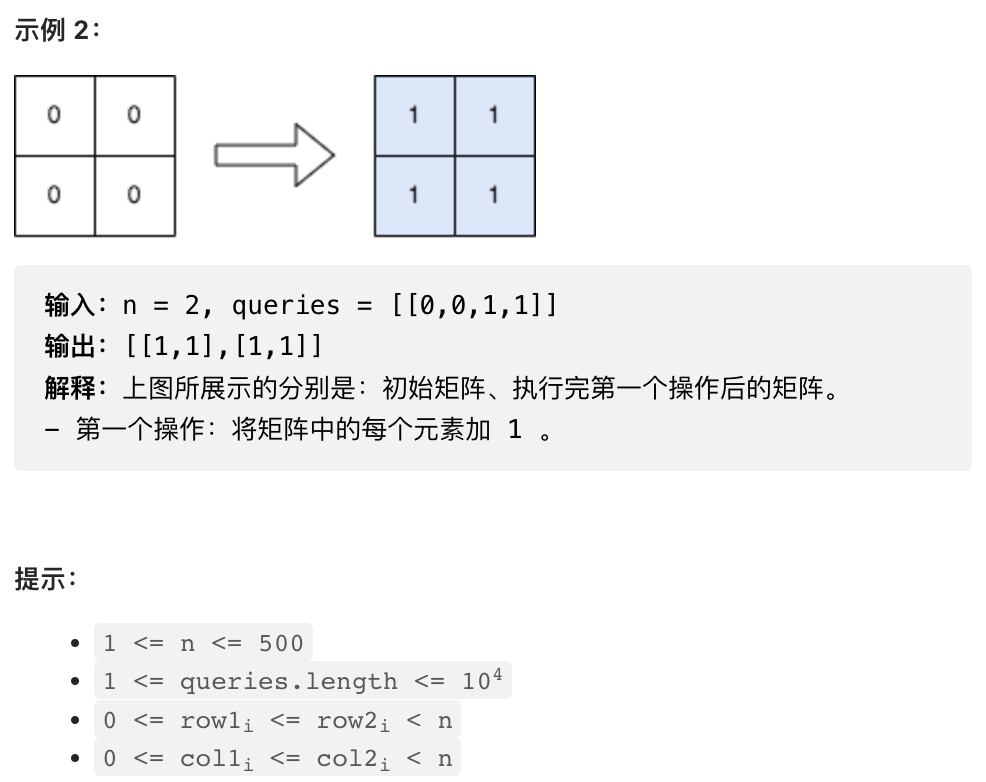
这道题目有点意思。很明显,直接暴力标记是不可行的,因为每次标记的区域可以很大,最终时间复杂度会是 O(n^2*m), m 是 Query 数量。
这里给出一种可能并非最优的 O(mn) 的做法,足够过掉这一道题目。基本思路是,对于每个 Query, 先在 Query 覆盖区域的每一行上标记起始和结束位置,全部 Query 标记完后再逐行运行类似于前缀和的算法即可。
class Solution:
def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
res = [[0] * n for _ in range(n)]
for r1, c1, r2, c2 in queries:
# 在 Query 覆盖区域标记每一行的开始和结束位置
# 注意这里的逻辑结束位置要标记在覆盖区域的下一格(前闭后开区间)
for r in range(r1, r2 + 1):
res[r][c1] += 1
if c2 + 1 < n:
res[r][c2 + 1] -= 1
for row in res:
pre = 0
for i in range(n):
# 类前缀和逻辑
# 第一轮标记直接标记在了 res 矩阵中,然后原地求前缀和
# 节省一点空间,并更加简洁,但实现时需要稍加小心,下方两行顺序不能颠倒
pre += row[i]
row[i] = pre
return res
class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> res(n, vector<int>(n));
for(auto& v: queries) {
// 在 Query 覆盖区域标记每一行的开始和结束位置
// 注意这里的逻辑结束位置要标记在覆盖区域的下一格(前闭后开区间)
for(int r = v[0]; r <= v[2]; r++) {
res[r][v[1]]++;
if(v[3] + 1 < n) {
res[r][v[3] + 1]--;
}
}
}
for(int r = 0; r < n; r++) {
int d = 0;
for(int c = 0; c < n; c++) {
// 类前缀和逻辑
// 第一轮标记直接标记在了 res 矩阵中,然后原地求前缀和
// 节省一点空间,并更加简洁,但实现时需要稍加小心,下方两行顺序不能颠倒
d += res[r][c];
res[r][c] = d;
}
}
return res;
}
};
3.

本题可以视为滑动窗口题目的变体。一个子列中相等数对的数量可以通过统计每个数字出现的次数得到。使用滑动窗口统计,当已经有 n 个数字时,再加入一个数字,增加的相等数对个数恰好是 n. 可以使用一个 map 来统计不同的数字出现的频次。
另外,由于本题要求统计所有满足条件的子列,枚举将会超时。这里使用一种滑动窗口题目中常见的技巧,我们固定右端点,然后寻找第一个【不】符合条件的左端点,然后这个端点左侧的端点都是符合条件的。
class Solution {
public:
long long countGood(vector<int>& nums, int k) {
unordered_map<int, int> win; // <数字,频次>
// total 是窗口中满足条件的数对总个数
long long res = 0, total = 0;
for(int left = 0, right = 0; right < nums.size(); right++) {
// 右端点入窗口,更新 win & total
// 注意 ++ 操作符在右侧时返回更新之前的值
total += win[nums[right]]++;
// 搜索第一个不符合条件的左端点
while(total >= k) {
// 左端点出窗口
// 注意 -- 操作符在左侧时返回更新之后的值
total -= --win[nums[left++]];
}
// left 左侧共有 left 个点
res += left;
}
return res;
}
};
4.
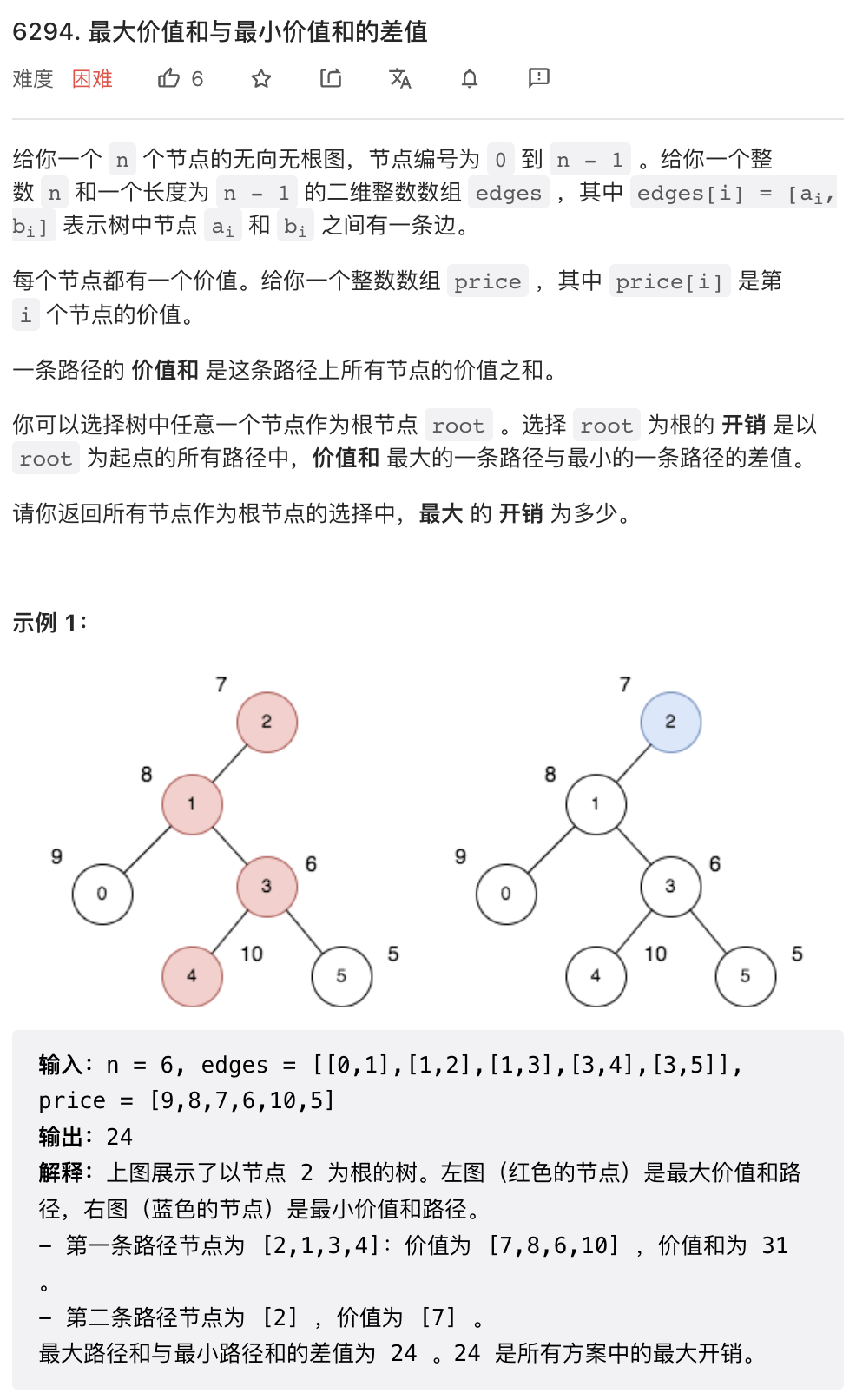
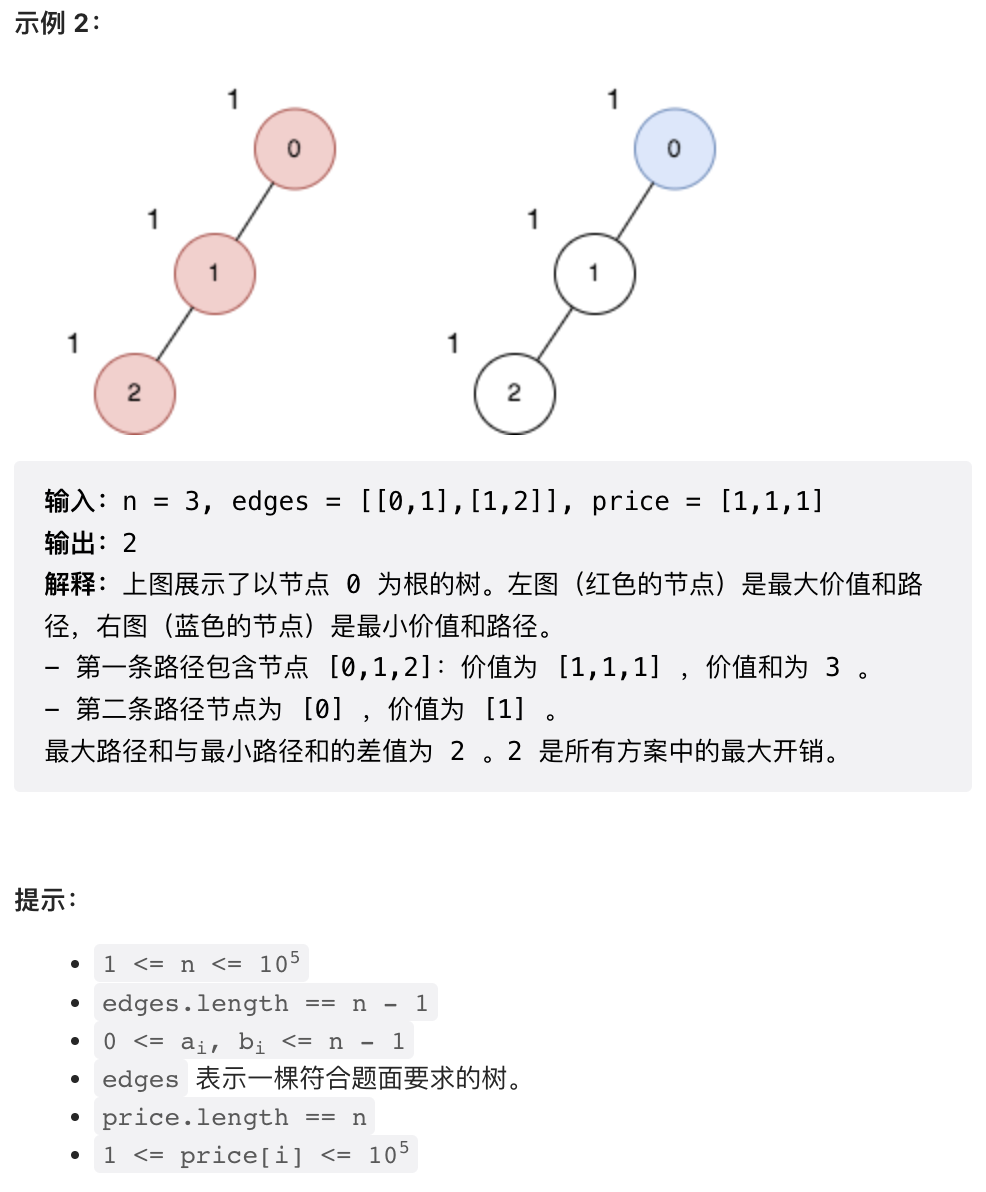
对于最大路径和的计算,考虑暴力计算,则需要以每个节点为根进行 DFS 求最长路径。这样会有大量重复计算。考虑 DFS 的过程,实际上当 parent 节点固定时,当前节点对应的子树搜索到的最大路径和就是固定的。因此,可以在 DFS 基础上进行自顶向下 DP, DP 空间就会是 (当前节点,parent 节点). 这个 pair 恰好是一条边,DP 状态就可以存储在边上。
这个问题的 DP 空间大小就是边的数量,时间复杂度也是 O(m), m 是边的数量。
这个解法实际上时间复杂度是有问题的。由于对每个状态的求解最多需要 O(m) 的时间复杂度,这个解法实际上是 O(m^2) 复杂度,这种复杂度在 n-1 个节点都连接到根节点时确实会出现。但由于 LeetCode 数据太弱,被我们水过去了。时间复杂度真正正确的接发可以参考:
https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/
最小路径和显然是根节点单个节点。
// 这个数据结构是重点!
// 一条边,<子节点 id, 该子节点作为 parent 节点的当前子树最长路径长度>
typedef pair<int, long long> Child;
// 一个节点的所有子节点
typedef vector<Child> ChildVec;
class Solution {
public:
long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
// 建图
vector<ChildVec> g(n);
for(auto& p: edges) {
g[p[0]].push_back({p[1], -1LL});
g[p[1]].push_back({p[0], -1LL});
}
// 将子节点排序,之后会使用二分法根据 ID 查找子节点
for(auto& v: g) {
sort(v.begin(), v.end());
}
// 穷举每个节点作为根节点时的最长路径
long long res = 0;
for(int i = 0; i < n; i++) {
res = max(res, dfs(g, price, i, -1) - price[i]);
}
return res;
}
// 求解指定 parent 节点时,node 节点对应的子树中最大路径和
// 对于根节点,parent = -1
long long dfs(vector<vector<pair<int, long long>>>& g, vector<int>& price, int node, int parent) {
// 使用二分法从近邻节点中找到 parent 节点,检查是否已经计算
ChildVec::iterator p;
if(parent != -1) {
p = lower_bound(g[node].begin(), g[node].end(), make_pair(parent, -1LL));
if(p->second != -1) {
return p->second;
}
}
// 如果没有计算,则递归计算所有子节点的最大路径和
long long res = 0;
for(auto& p: g[node]) {
if(p.first != parent) {
res = max(res, dfs(g, price, p.first, node));
}
}
// 更新 DP 状态,返回结果
res += price[node];
if(parent != -1) {
p->second = res;
}
return res;
}
};