本周周赛有两道 Hard! 两道题难度中规中矩,分别是巨烦无比的分类讨论 & 暴力版本公共祖先。
1.


非常简单的一道题目。
题目中其实定义了一种「相等」关系。对这类题目,我比较喜欢的一种 O(n) 时间复杂度的做法是,为每一类相等关系选取一个代表元作为 key, 然后数一下每个 key 出现的次数就行了。本题「代表元」可以选取将 word 所有字母去重排序后的字符串。
class Solution:
def similarPairs(self, words: List[str]) -> int:
# 计数每个代表元所在的彼此相等集合中元素个数
cnt = collections.Counter("".join(sorted(set(s))) for s in words)
# 每个集合提供的 pair 是 x * (x - 1) / 2
return sum(x * (x - 1) // 2 for x in cnt.values())
2.

这是一个很不像 LeetCode 风格的「数论」题目,你需要了解质因数分解算法。这里直接给出一个比较快的质因数分解算法模板。由于这个模板是 CPP 的,这道题目就 CPP 了。
质因数分解是 O(n ^ 0.5) 的时间复杂度。这道题目每次操作直觉上会令 n 的值以接近 log n 的程度衰减(好像不难证明,留给读者试试),所以这个平方根时间复杂度的质因数分解算法 + 暴力迭代就够了。
// worst complexity: O(num ^ 0.5)
template <typename NUM = int>
void prime_fact(NUM num, vector<NUM>& res) {
while (num % 2 == 0) {
num /= 2;
res.push_back(2);
}
for (int p = 3; p * p <= num; p += 2) {
while (num % p == 0) {
res.push_back(p);
num /= p;
}
}
if (num > 1) res.push_back(num);
}
class Solution {
public:
int smallestValue(int n) {
vector<int> fact;
while(true) {
fact.clear();
prime_fact(n, fact);
int _n = accumulate(fact.begin(), fact.end(), 0);
if(_n == n) break;
n = _n;
}
return n;
}
};
3.
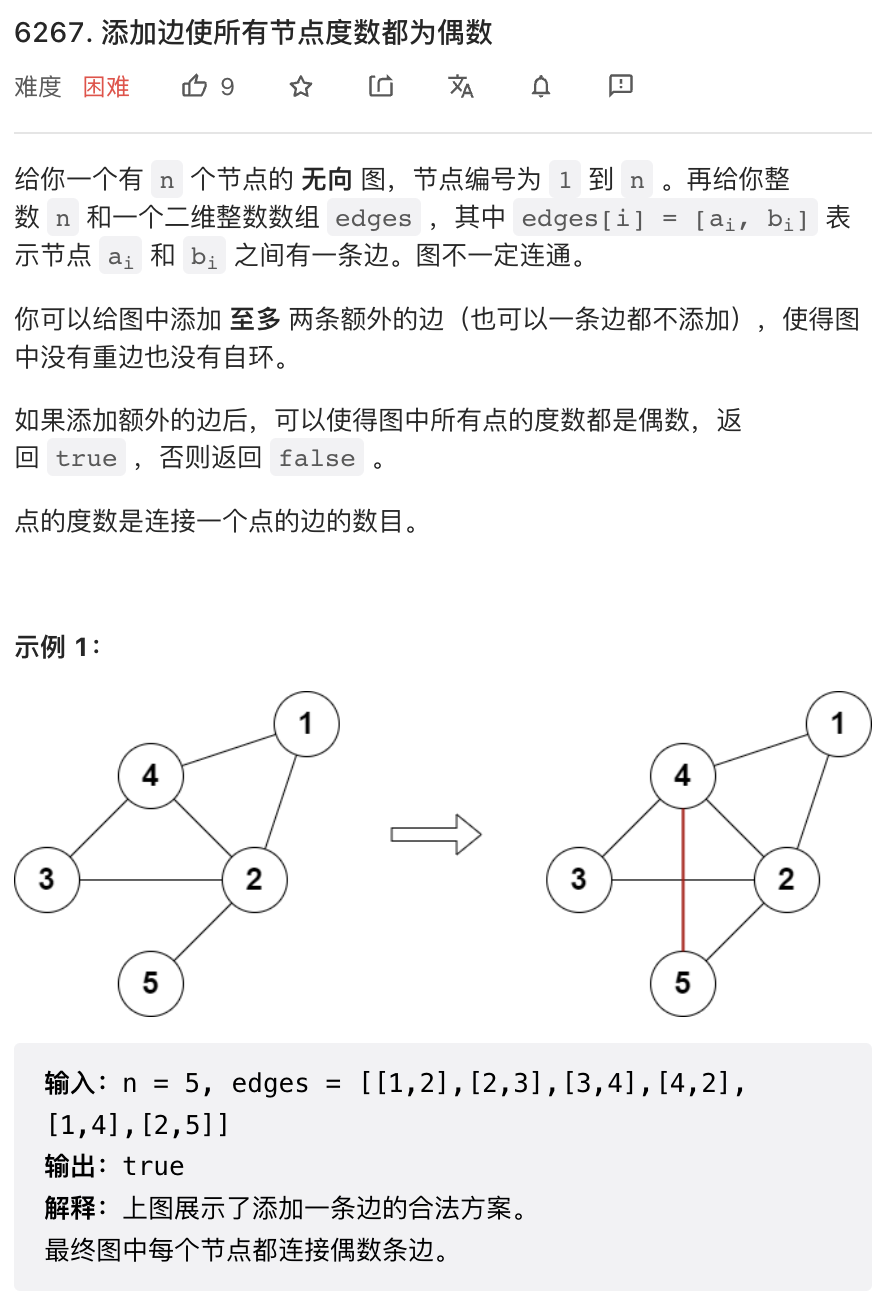
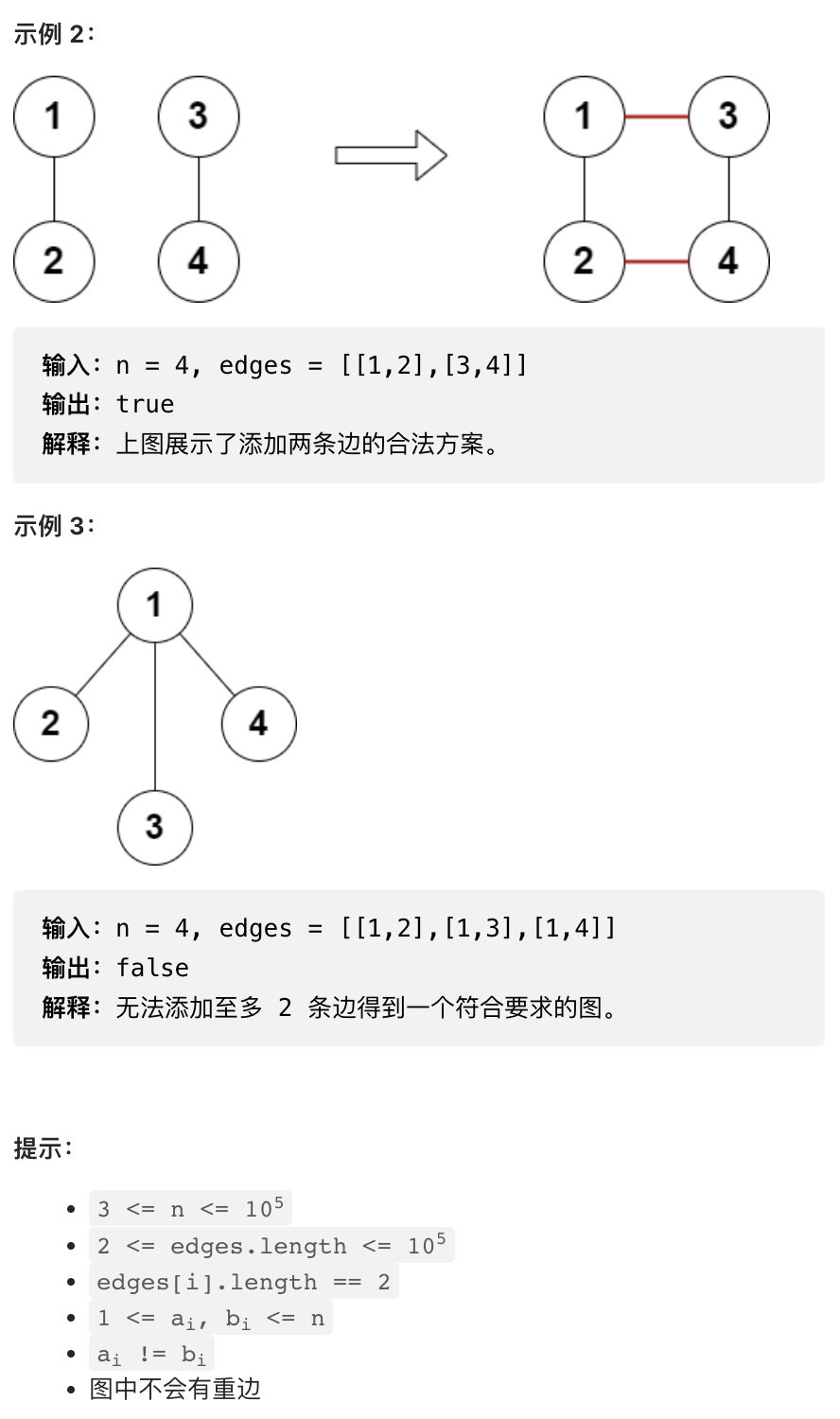
这是一道我最讨厌的题目,仔细看了好多遍,好像确实不难,但也没啥漂亮解法,是一个比较麻烦的分类讨论,要写很多 if else.
基本思路是,原图中最多可以有四个度数为奇数的节点,然后根据节点个数展开分类讨论。在尝试加入新的边时需要检查是否重复,所以需要把所有的边加到一个 set 里。
class Solution {
public:
bool isPossible(int n, vector<vector<int>>& edges) {
// 统计度数
vector<int> degree(n + 1);
// 边 set, 用于检查边是否已经存在
// 总是把边较小的节点放在前面
set<pair<int, int>> es;
for(auto& p: edges) {
degree[p[0]]++;
degree[p[1]]++;
es.insert({min(p[0], p[1]), max(p[0], p[1])});
}
// 所有度数为奇数的候选节点
vector<int> can;
for(int i = 1; i <= n; i++) {
if(degree[i] % 2) {
can.push_back(i);
}
}
// 没有度数为奇数的节点,无需操作
if(can.size() == 0) {
return true;
}
if(can.size() == 2) {
// 两个奇数度数节点
// 如果这两个节点之间没有变,则加一条边即可
if(!es.count({can[0], can[1]})) {
return true;
}
// 否则,需要另找一个节点,然后分别跟这个节点加一条边
// 所以需要 can 中两个节点跟这个节点都没有边相连
for(int j = 1; j <= n; j++) {
if(j != can[0] and j != can[1]) {
auto p1 = make_pair(min(can[0], j), max(can[0], j));
auto p2 = make_pair(min(can[1], j), max(can[1], j));
if(!es.count(p1) and !es.count(p2)) {
return true;
}
}
}
} else if(can.size() == 4) {
// 四个奇数节点,则必须能够两两加一条边
if(
(!es.count({can[0], can[1]}) and !es.count({can[2], can[3]})) or
(!es.count({can[0], can[2]}) and !es.count({can[1], can[3]})) or
(!es.count({can[0], can[3]}) and !es.count({can[1], can[2]}))
) {
return true;
}
}
// 其他情况都不行
return false;
}
};
4.


第四题难度感觉比第三题难度小一点。要求的环的长度,其实就等于这两个节点到「最近公共祖先」距离之和加一。由于这是一棵满树,高度最多 30, 所以可以暴力求解最近公共祖先。而且这个满树可以根据节点编号方便的求出节点深度,从而很容易判断两个节点是不是在同一层。
class Solution {
public:
vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {
vector<int> res;
for(auto &p: queries) {
int x = min(p[0], p[1]), y = max(p[0], p[1]);
int r = 1;
// y 编号总是大于 x,所以层数总是比 x 更深
// 如果 y 与 x 不在同一层,则先把 y 提升到跟 x 同一层
// '>>= 1' 即父节点
while(level(y) > level(x)) {
y >>= 1;
r++;
}
// 两者在同一层,则一直上移直到到达公共祖先
while(x != y) {
y >>= 1;
x >>= 1;
r += 2;
}
res.push_back(r);
}
return res;
}
// 求节点层数,观察一下不难发现,节点层数也即节点编号的最高有效位位置
int level(int x) {
for(int m = 1; m <= 30; m++) {
if(x < (1 << m)) {
return m;
}
}
return 31;
}
};