本周双周赛第一题非常适合做小学生数学题,第四题是个也很有意思的动态规划。
1.
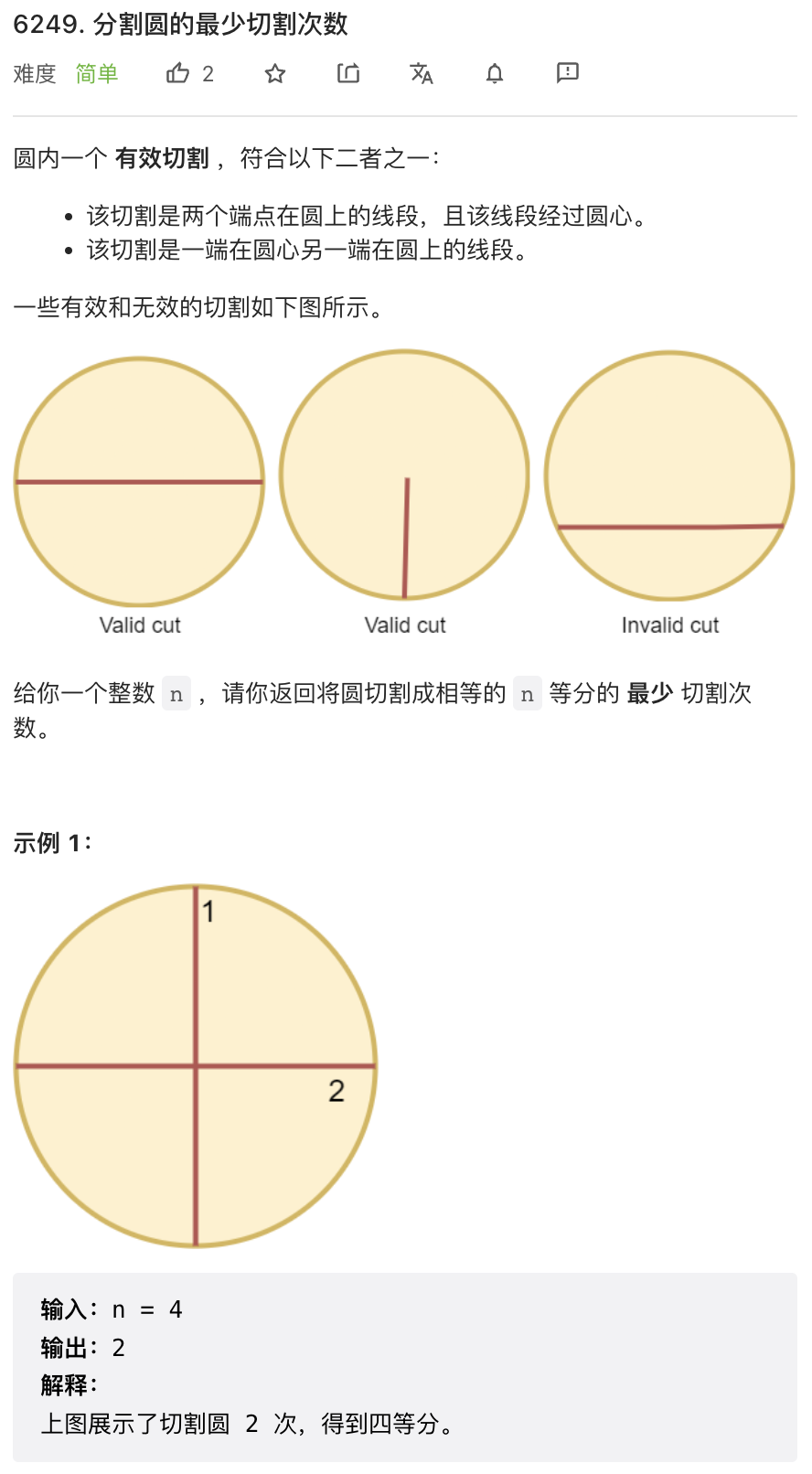
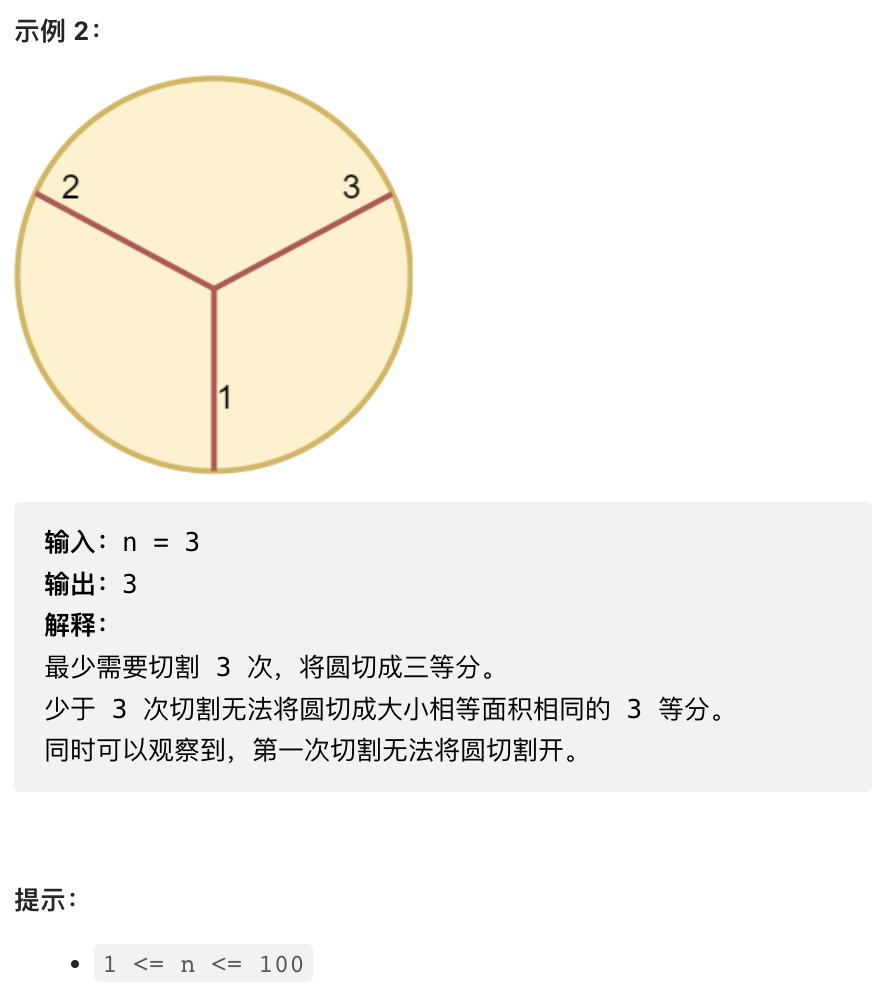
这个题目需要稍微开动一下脑筋,分为三种情况:
- 如果最终需要划分奇数份,则每份都需要一刀
- 如果是偶数份,则只需要
n/2刀 - 特别的,如果是一份,答案是 0 刀
class Solution:
def numberOfCuts(self, n: int) -> int:
return 0 if n <= 1 else n if n % 2 else n // 2
2.


本题非常简单,按要求计算即可。首先统计一下每一行 0 和 1 的数量,然后按照公式计算即可。
一个小优化是,只需要统计 0 的数量,1 的数量可以用总数减去 0 的数量。
class Solution:
def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:
m, n = len(grid), len(grid[0])
row0, col0 = [0] * m, [0] * n
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
row0[i] += 1
col0[j] += 1
res = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
res[i][j] = m + n - 2 * row0[i] - 2 * col0[j]
return res
3.


同样非常简单的第三题。在某一时刻关门的 cost, 就等于之前时刻 N 的前缀和,以及之后时刻 Y 的后缀和。
后者可以用前缀和推算出来。如果不想费劲推算,也可以暴力把 Y 后缀和算出来。
class Solution:
def bestClosingTime(self, customers: str) -> int:
n = len(customers)
pre_n = [0] * (n + 1)
for i in range(n):
pre_n[i + 1] = (customers[i] == 'N') + pre_n[i]
res = 0
min_cost = n
for i in range(n + 1):
# suf_y[i] = total_y - pre_y[i]
# = n - pre_n[n] - (i - pre_n[i]) = n - pre_n[n] - i + pre_n[i]
# cost = pre_n[i] + suf_y[i]
# = n - i - pre_n[n] + 2 * pre_n[i]
cost = n - i - pre_n[n] + 2 * pre_n[i]
if cost < min_cost:
min_cost, res = cost, i
return res
4.

第四题不是很难,有点意思。这个题目要求字符串中长度为 5 的回文子序列个数,而且字符串中只有数字。
长度为 5 回文子序列,意味着选定中间字符之后,前后只有两个字符需要决定了。再有限制字符串中只有数字,注意数据规模 1E4 这个问题很有可能是个 O(100N) 的复杂度。
一个可行的办法是,我们可以计算每个位置其前方或者后方所有长度为 2 的子序列个数,子序列最多只有 100 种,然后每个位置统计其前后匹配的子序列个数相乘就可以了。而长度为 2 的子序列个数,可以根据每个位置前方每个字符的计数再加一层统计即可。具体逻辑我在代码里写了详细的注释。
由于担心 Python 超时,这个题目给出 C++ 代码。
class Solution {
public:
int countPalindromes(string s) {
int n = s.size();
long long mod = 1E9 + 7;
// pre 是每个字符个数的前缀和,注意 pre[i] 是 s[:i-1] 的前缀和
vector<vector<long long>> pre(n + 1, vector<long long>(10));
// pre2[i] 是 s[:i-1] 之中,每种长度为 2 的子序列的计数
// s[:i-1] 中一个 "12" 子序列会记录在 pre2[i][12] 中
vector<vector<long long>> pre2(n + 1, vector<long long>(100));
// 后缀和
// suf2 与 pre2 类似,但子序列自带一个反向,也即子序列 "12" 的下标是 21
// 这样最后进行匹配时,只要值相等就可以了
auto suf = pre, suf2 = pre2;
for(int i = 0, j = 1; i < n; i++, j++) {
// 前缀和
copy(pre[i].begin(), pre[i].end(), pre[j].begin());
copy(pre2[i].begin(), pre2[i].end(), pre2[j].begin());
int c = s[i] - '0';
// 更新 pre
pre[j][s[i] - '0']++;
// 更新以当前字符结尾的长度为2子序列个数
for(int x = 0; x <= 9; x++) {
pre2[j][x * 10 + c] += pre[i][x];
}
}
// 跟前缀和对称的后缀和逻辑
for(int i = n, j = n - 1; i > 0; i--, j--) {
copy(suf[i].begin(), suf[i].end(), suf[j].begin());
copy(suf2[i].begin(), suf2[i].end(), suf2[j].begin());
int c = s[j] - '0';
suf[j][c]++;
for(int x = 0; x <= 9; x++) {
suf2[j][x * 10 + c] += suf[i][x];
}
}
long long res = 0;
for(int i = 0; i < n; i++) {
// i 是回文子串中心,以 i 为中心的回文子串数量就是
// 前后匹配的子串数量相乘再求和
for(int x = 0; x <= 99; x++) {
res = (res + pre2[i][x] * suf2[i + 1][x]) % mod;
}
}
return int(res);
}
};