本次周赛给我的感觉是,除第四题外过于简单。第四题是一个稍微有点复杂的 DP。
1.

非常简单,直接实现。可能存在更优算法,但没什么必要。
class Solution:
def unequalTriplets(self, nums: List[int]) -> int:
n = len(nums)
cnt = 0
for i in range(n):
for j in range(i + 1, n):
for k in range(j + 1, n):
cnt += nums[i] != nums[j] and nums[i] != nums[k] and nums[j] != nums[k]
return cnt
2.
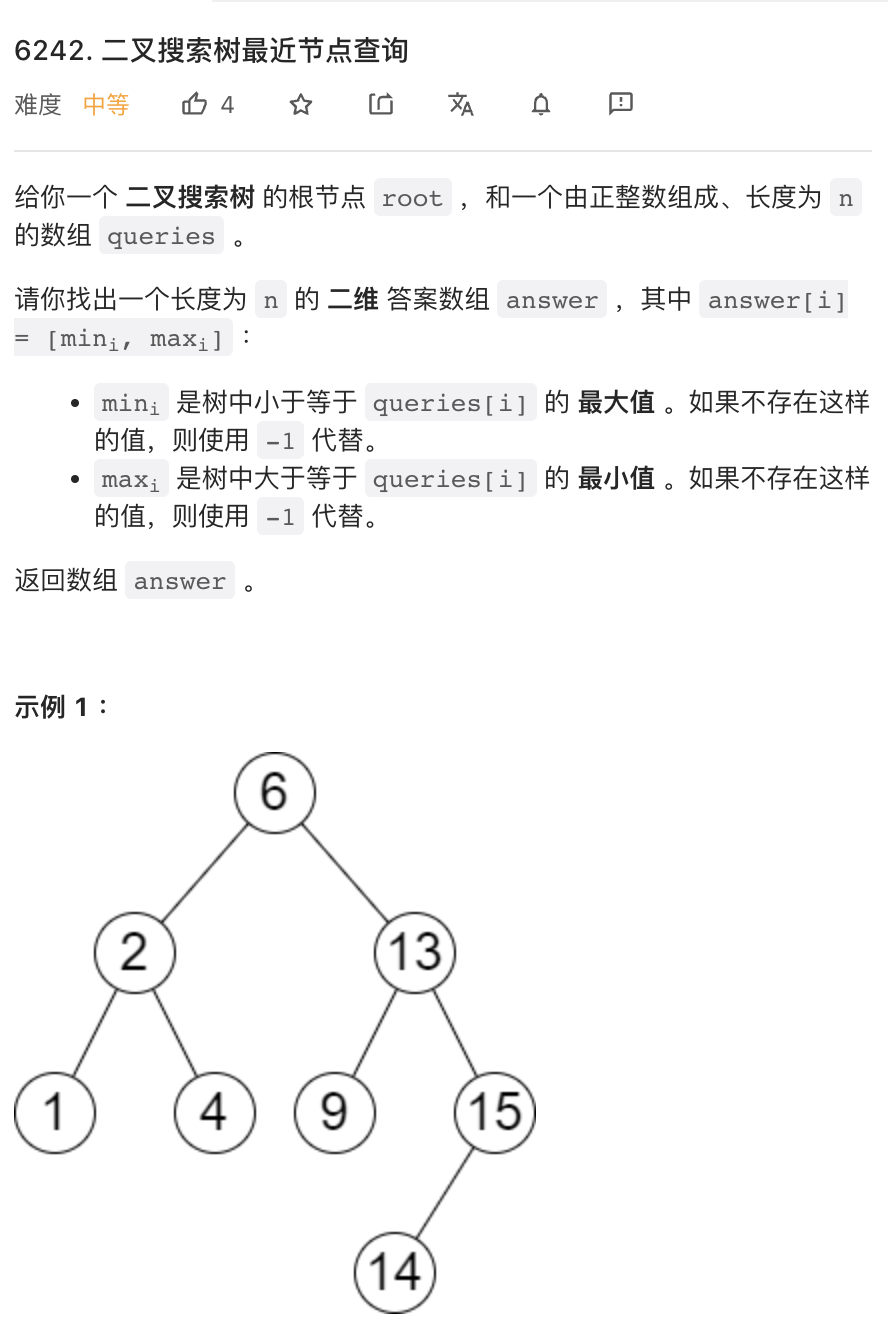

这个题目吧,如果出现在面试中,面试官的意思肯定是让你在树上进行操作,完成他的要求。但是出现在网测中,那就是另一回事了:二叉搜索树有可能严重不平衡,导致搜索复杂度达到 O(n) 因此有超时风险。
于是,更稳妥的做法是,先中序遍历二叉搜索树,把所有节点保存在一个数组中,然后使用二分查找。
使用二分查找时,注意仔细检查二分查找的 API,这个比较容易写错。多写几个 if else 虽然丑但是保险。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:
# 中序遍历二叉搜索树
nums = []
def inOrder(node):
if node:
inOrder(node.left)
nums.append(node.val)
inOrder(node.right)
inOrder(root)
n = len(nums)
res = []
for x in queries:
# p 是 nums 中第一个大于等于 x 的数的下标,相当于 C++ 的 lower_bound
p = bisect.bisect_left(nums, x)
if p != n and nums[p] == x:
# nums 中存在 x 则上下限都是 x
res.append([x, x])
elif p == n:
# nums 中不存在大于等于 x 的数
res.append([nums[p - 1], -1])
elif p == 0:
# nums 中不存在小于等于 x 的数(等于第一个 if else 覆盖了)
res.append([-1, nums[p]])
else:
# 正常情况
res.append([nums[p - 1], nums[p]])
return res
3.

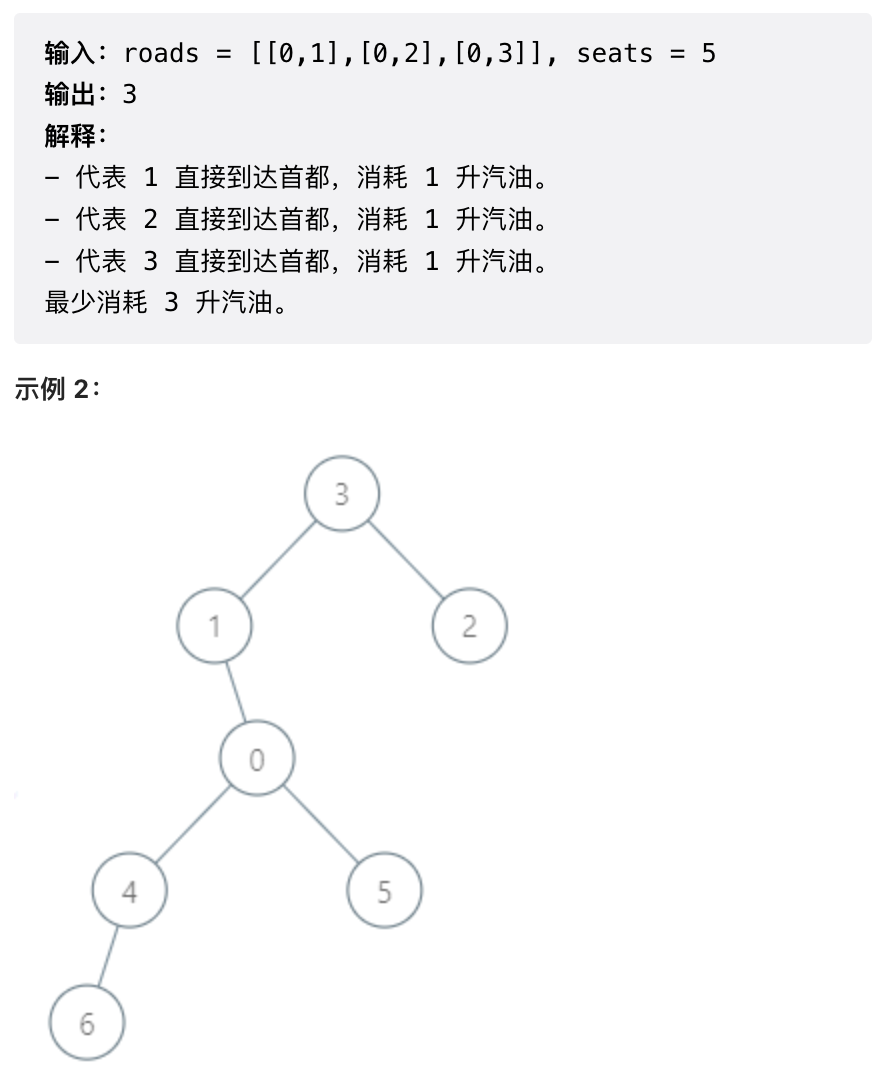

感觉这个问题作为第三题而言有些简单了。其实就是统计一下树上每个节点有多少个子节点,然后除以 seats 向上取整就是从这个节点到下一个父节点的 cost. 每个节点的 cost 分别计算即可。
class Solution:
def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
n = len(roads) + 1
# 构建树
g = [[] for _ in range(n)]
for x, y in roads:
g[x].append(y)
g[y].append(x)
def dfs(node, parent):
# total: node 的子节点数量,包含自身
# subcost: 所有子节点移动到该节点的开销
total = subcost = 0
for child in g[node]:
if child != parent:
t, s = dfs(child, node)
total += t
subcost += s
total += 1
if node != 0:
# 如果当前不是根节点,则再加上前往父节点的开销
# 整数上取整除法
subcost += total // seats + 1 if total % seats else total // seats
return total, subcost
return dfs(0, -1)[1]
4.


这个问题是个稍微有点复杂的 DP.
这种连续区间问题很容易想到使用 DP 求解,使用 DP 计算所有前缀,所有 k 值对应的分割数量。DP 空间大小是 O(n^2). DP 递推公式也即最后一个区间枚举所有可能的长度即可。但如果暴力枚举,则递推公式复杂度也是 O(n) 最终复杂度不可接受,因此我们需要使用一个类似于前缀和的方法加速。代码中有详细的注释。
这个问题稍微有点难度,难度就在于搞清楚这个前缀和应该怎么定义,并且在 DP 递推过程中处理好这个前缀和。
写这类 DP 问题,我的技巧是,一般写 bottom-up DP,并按照以下顺序写代码,而不是从头到尾一遍写出来。
- 定义好 DP 状态
- 写 DP 推导代码
- 检查 DP 状态依赖关系,并确认能够满足 DP 状态求解顺序
- 检查边界条件处理,包括 DP 边界状态的处理
class Solution:
def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:
p = "2357"
mod = 10 ** 9 + 7
n = len(s)
# cnt[i][j]: 前 i 个字符(包括)分割为 j 个子串的方法数
cnt = [[0] * (k + 1) for _ in range(n)]
# 这个是重点,
# pre[i][j]: 终止在第 i 个字符(包括)之前,分割为 j 个子串,
# 并且其末尾字符的下一个字符是质数的方案数
# 因为是所有的「i 之前」因此是个前缀和
# 这个前缀和的用途可以参照下文的计算代码理解
pre = [[0] * (k + 1) for _ in range(n)]
for i in range(n):
if i != 0:
# 初始化前缀和
for j in range(1, k + 1):
pre[i][j] = pre[i - 1][j]
# 仅当 s[i] 是一个合法结尾时才计算 cnt[i][j]
if s[i] not in p:
# 仅有一个区间的边界状态
cnt[i][1] = 1 if s[0] in p and i >= minLength - 1 else 0
for j in range(2, k + 1):
# 递推公式
# cnt[i][j] 也即终止在 i - minLength 之前
# 的分割方案的前缀和
cnt[i][j] = pre[i - minLength][j - 1]
if i < n - 1 and s[i + 1] in p:
# 如果下一个字符是质数,更新前缀和
for j in range(1, k + 1):
pre[i][j] += cnt[i][j]
pre[i][j] %= mod
return cnt[n - 1][k] % mod
由于工作之后没空刷题,水平急剧下降,今天周赛久违的进了前百,可喜可贺。