复习很多生僻知识点,LCM,排序最小操作数。Python 还是容易超时,C++ 还是靠谱。
1. 温度转换

非常简单,直接实现。
class Solution:
def convertTemperature(self, celsius: float) -> List[float]:
return [celsius + 273.15, celsius * 1.80 + 32.00]
2. 最小公倍数为 K 的子数组数目

通常最大公约数用的比较多,最小公倍数用的比较少,这里复习一下。
最小公倍数跟最大公约数一样,如果视为二元运算符,具有交换律和结合律。本题中用到的性质是,最小公倍数跟前缀和一样,可以前缀计算。
Python 有内置的最小公倍数实现。如果要自行实现最小公倍数也不困难。
# 使用 gcd 实现 lcm
# def lcm(x, y):
# return x * y / gcd(x, y)
class Solution:
def subarrayLCM(self, nums: List[int], k: int) -> int:
n = len(nums)
total = 0
for left in range(n):
l = nums[left]
for right in range(left, n):
l = math.lcm(l, nums[right])
total += l == k
return total
3. 逐层排序二叉树所需的最少操作数目
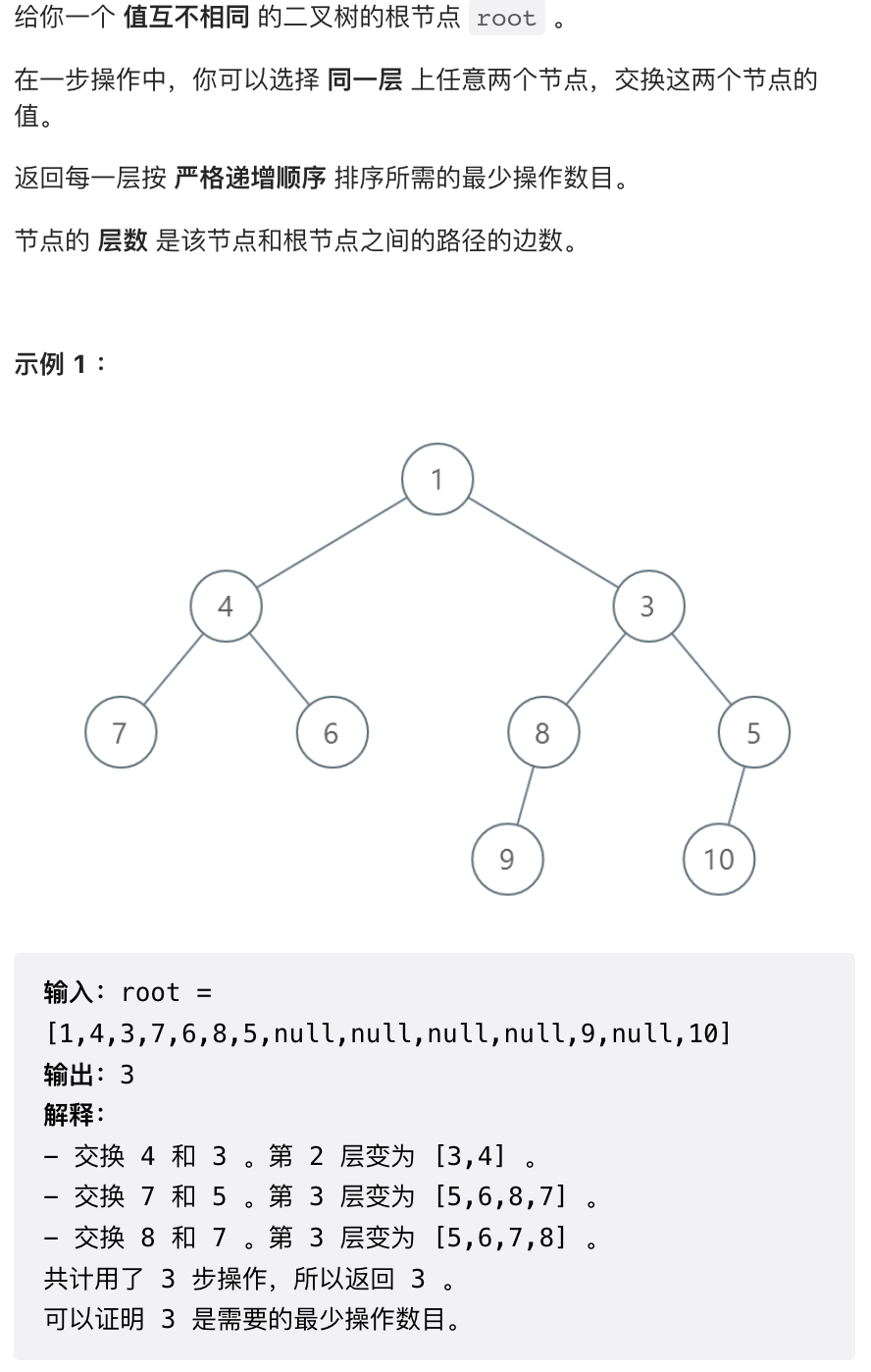
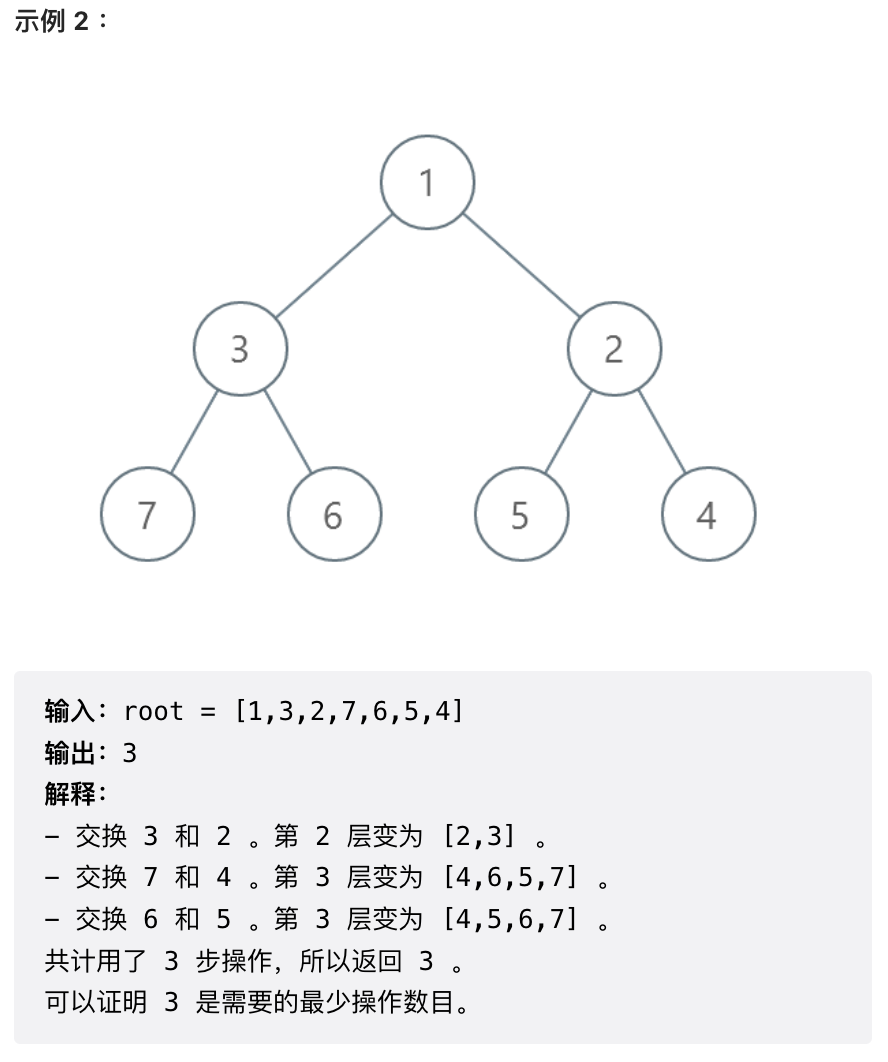
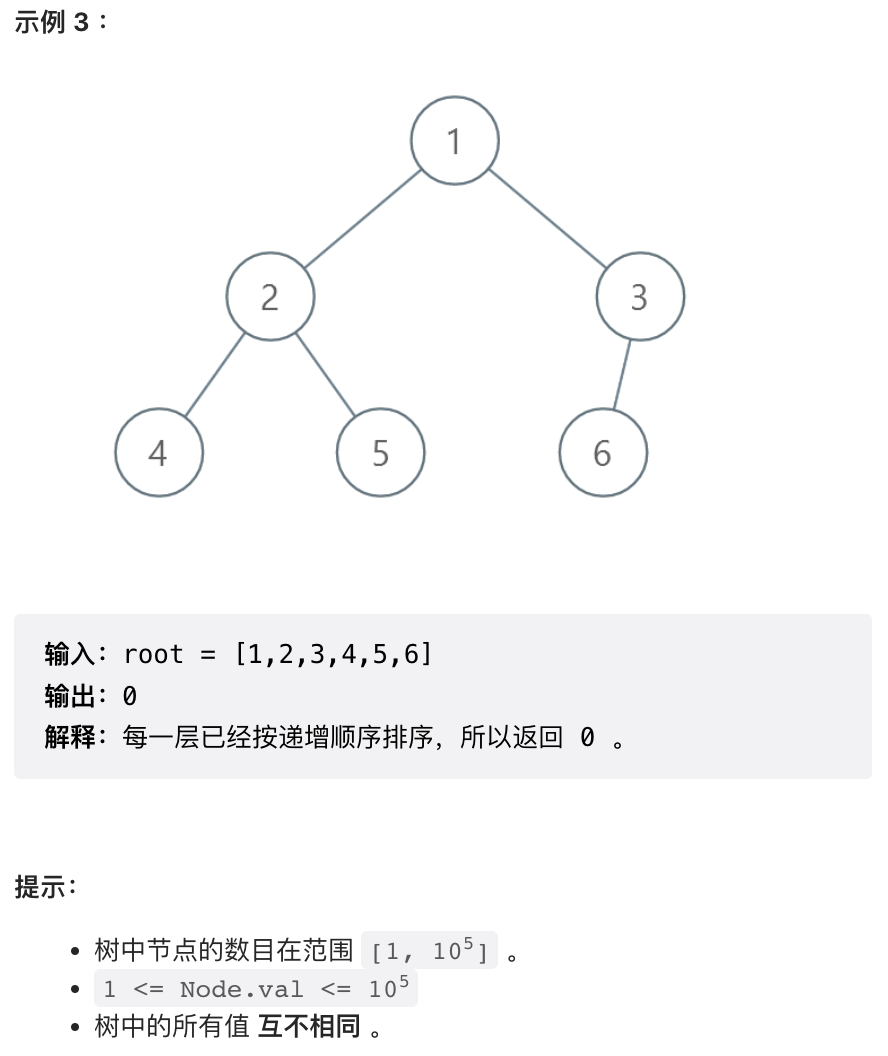
本题复习数组排序的最小操作数。
求排序的最小操作数有两种方法,一种做法是,先把这个数组排序,于是我们就知道了每个元素应该在最终的位置。然后从第一个位置开始,将应该在这个位置的数 y(最小元素)与该位置的数 x 交换。然后对于继续在 x 所在的位置执行这个操作,把应该放在这个位置的数换过来,把 x 换过去。重复该操作直到 x 恰好在它该在的位置。
另一种方法则是我这里使用的方法,借助并查集,对排序之后的数组和元素组,位置相同的元素标记为同一个集合。最后统计一下每个集合大小,将每个集合复原需要的操作数量就是集合大小减一。
这两种解法的背后的道理是相同的。我们将每个数字排序之后应该处的位置称为「目标位置」。数字x 的目标位置上的数字 y,其目标位置上有个数字 z … 最终这会构成一个环,这个环中如果有 n 个元素,则 n - 1 次操作就能把所有的元素归位。第一种方法就是模拟这个操作过程,第二种方法直接把这些环找出来。
本题中特别注意,没有必要逐层求解这个问题,可以所有层共用一个并查集。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minimumOperations(self, root: Optional[TreeNode]) -> int:
# 将每一层节点值分别加入 list
# 并统计一下最大节点值
max_node = 0
levels = collections.defaultdict(list)
def dfs(node, lv):
nonlocal max_node
if node:
levels[lv].append(node.val)
max_node = max(max_node, node.val)
dfs(node.left, lv + 1)
dfs(node.right, lv + 1)
dfs(root, 0)
# 并查集
mfs = list(range(max_node + 1))
# 并查集路径压缩查找函数
def find(x):
mfs[x] = x if mfs[x] == x else find(mfs[x])
return mfs[x]
# 构造所有的环
for nums in levels.values():
for x, y in zip(nums, sorted(nums)):
mfs[find(y)] = find(x)
# 统计环中元素数量
cnt = [0] * (max_node + 1)
for x in range(max_node + 1):
cnt[find(x)] += 1
# 每个环需要的操作数是元素数量 -1
return sum(x - 1 for x in cnt if x > 0)
4. 不重叠回文子字符串的最大数目

这个题目的数据规模有点尴尬,C++ O(n^2) 可以过,但 Python 不行。这个题目 O(n^2) 解法难度比第三题要低。
如果使用 O(n^2) 解法,该题目非常简单。首先上个回文子串判定,把所有的回文子串找出来。然后 DP 即可。
# 该代码超时,C++ 版本可以过
class Solution:
def maxPalindromes(self, s: str, k: int) -> int:
n = len(s)
# 判定所有回文子串
pali = [[True] * (n + 1) for _ in range(n + 1)]
for i in range(n - 1, -1, -1):
for j in range(i + 1, n):
pali[i][j] = pali[i + 1][j - 1] and s[i] == s[j]
# dp[i] 是前缀 s[:i+1] 中的子字符串最大数目
dp = [0] * n
for right in range(n):
if pali[0][right] and right >= k - 1:
# 如果本身是个合法子字符串,则最大数据初始化为 1
dp[right] = 1
# 枚举以 right 结尾的所有子字符串
for left in range(right - 1, -1, -1):
# 判断 s[left+1:right+1] 是否为合法子字符串
suf = right - left >= k and pali[left + 1][right]
# dp 推导公式
dp[right] = max(dp[right], dp[left] + suf)
if suf:
# dp 是单调递增的
# 所以寻找到第一个合法位置之后可以提前退出
break
return dp[-1]
class Solution {
public:
int maxPalindromes(string s, int k) {
int n = s.size();
vector<vector<bool>> pali(n + 1, vector<bool>(n + 1, true));
for(int i = n - 1; i >= 0; i--) {
for(int j = i + 1; j < n; j++) {
pali[i][j] = pali[i + 1][j - 1] and s[i] == s[j];
}
}
vector<int> dp(n);
for(int right = 0; right < n; right++) {
if(pali[0][right] and right >= k - 1) {
dp[right] = 1;
}
bool suf = false;
for(int left = right - 1; left >= 0 and not suf; left--) {
suf = right - left >= k and pali[left + 1][right];
dp[right] = max(dp[right], dp[left] + suf);
}
}
return dp.back();
}
};