本周双周赛难度一般,第三题和第四题难度差不多,第三题甚至要麻烦一些。
1. 不同的平均值数目

按照要求操作即可。注意两个要点:
- 不同平均值个数等于不同的和的个数,借此避免浮点除法
- 除法运算有浮点误差的风险(不过实际上本题处以 2 并不会触发浮点计算误差)
- 这里给出的代码每个平均值计算了两遍,并不影响结果
class Solution:
def distinctAverages(self, nums: List[int]) -> int:
nums.sort();
return len(set(x + y for x, y in zip(nums, nums[::-1])))
2. 统计构造好字符串的方案数

一个非常简单、非常典型的 DP,很适合用作大学一年级学完 DP 之后的课后练习的第一题。
反复确认了好几遍这个 0 和 1 没啥特别之处。
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
mod = 10 ** 9 + 7
dp = [1] + [0] * (high)
for i in range(1, high + 1):
dp[i] += dp[i - zero] if i - zero >= 0 else 0
dp[i] += dp[i - one] if i - one >= 0 else 0
dp[i] %= mod
return sum(dp[low:high + 1]) % mod
3. 树上最大得分和路径

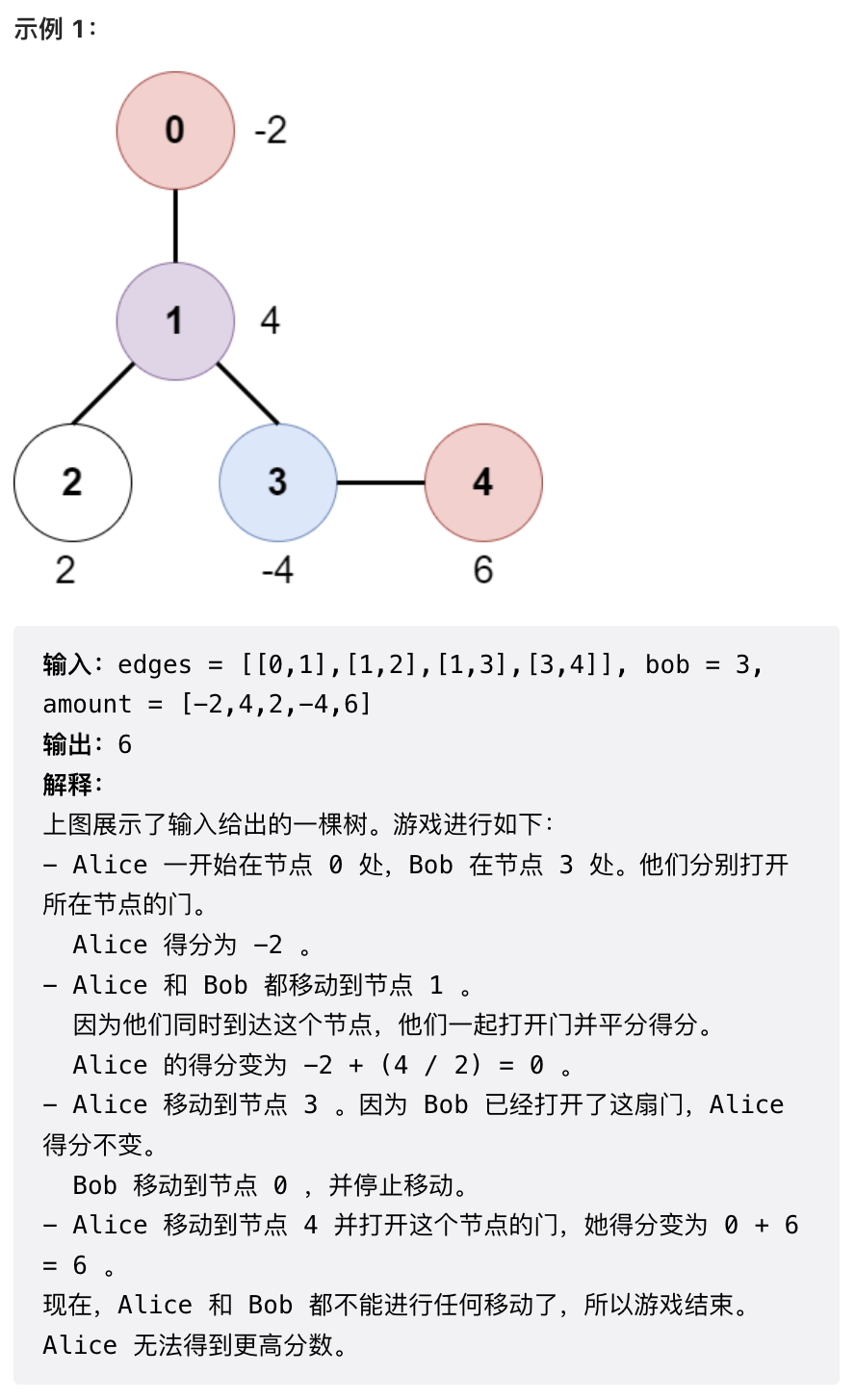

这个题目讨论区有人认为作为第三题太难了。实际上这个题目只是稍微麻烦了一点,一点都不难。
这个题目比较简单的点在于,由于给定的是无向树而不是图,所以任意两个节点之间路径存在且唯一。因此,Bob 的路是完全确定的,可以先把 Bob 的路径标记出来,包括他到达路径上每一个点的时刻。而 Alice 前往任意一个叶节点的路径也是唯一的,可以用一个 DFS 遍历一遍图,把 Alice 的路径全部找出来,并在遍历过程中处理与 Bob 相交的节点。
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
n = len(amount)
# 建图
graph = [[] for _ in range(n)]
for x, y in edges:
graph[x].append(y)
graph[y].append(x)
# 求以 0 为根节点时,每个节点的父节点
# bob 的路径就是每次前往父节点,直到到达 0
parent = [-1] * n
def get_parent(node, p):
parent[node] = p
for child in graph[node]:
if child != p:
get_parent(child, node)
get_parent(0, -1)
# 求 bob 到达其路径上的每个节点的时刻
# 未到达节点时刻标记为 n
t = 0
visit = [n] * n
while bob != -1:
visit[bob] = t
t += 1
bob = parent[bob]
# 标记 alice 到达每个叶节点时总得分
# node: 当前节点
# parent: dfs 路径的上一个节点
# time: 也即 dfs 深度
# got: 路径总得分
# result: 记录叶节点总得分的数组
def dfs(node, parent, time, got, result):
if visit[node] > time:
# bob 未曾到达
got += amount[node]
elif visit[node] == time:
# 与 bob 同时到达
got += amount[node] // 2
# 先假设这是个叶节点,更新得分
result[node] = got
for child in graph[node]:
if child != parent:
dfs(child, node, time + 1, got, result)
# 如果有任意一个字节点,则说明这不是个叶节点,删除得分
result[node] = float("-inf")
# 得分初始化为 -inf 因为这个问题中得分可以为负数
res = [float("-inf")] * n
dfs(0, -1, 0, 0, res)
return max(res)
4. 根据限制分割消息

从各个角度来说,这个问题都不是很难。我给出的解法也不是最优的,但思路比较简单。
这种复杂的字符串操作问题最好使用 Python 实现。这个问题的难点在于,不同的总消息数下后缀长度不同,每一个部分由于序号不同,后缀长度也不同。
思路上最简单的做法是,只要确认了总消息数长度,分割方法就几乎确定了,因此可以尝试总消息数为 9, 99, 999 等等,如果能够成功分割,再按照真实的分割数量重新生成一遍。
这个代码比较浪费,在尝试时不必生成字符串,只需要检查合法与否就可以了。但因为数据规模不大、O(n) 算法,这样也是可以的。
class Solution:
def splitMessage(self, message: str, limit: int) -> List[str]:
# 一个数字的十进制表示长度
# 直接使用 len(str(x)) 也可以,但开销比较大
def slen(x):
return 1 if x < 10 else 2 if x < 100 else 3 if x < 1000 else 4 if x < 10000 else 5
# 按照总数为 n_part 尝试进行分割
def check(n_part):
n_part_len = slen(n_part)
message_len = len(message)
# idx 是下一个需要分配的字符
idx = 0
res = []
while idx < message_len and len(res) < n_part:
cost = 3 + n_part_len + slen(len(res) + 1)
if cost >= limit:
# 后缀大于等于 lim 则无法分割
return []
used = limit - cost
# 生成一个分割
res.append("%s<%s/%s>" % (message[idx:idx + used], len(res) + 1, n_part))
idx += used
# 检查是否合法并返回
return res if idx >= message_len and len(res) <= n_part else []
# 尝试总长度为 9, 99, 999 等等
# 最大尝试 9999, 如果仍然无法分割,则一定无法分割,因为 len(s) < 1e4
curr_total = 9
while slen(curr_total) < 5:
res = check(curr_total)
if res:
# 一旦分割成功,则按照真实长度重新生成一次
res = check(len(res))
return res
curr_total = curr_total * 10 + 9
return []