本周周赛难度尚可,第四题比较有意思。
1. 可被三整除的偶数的平均值

能够被 3 整除的偶数,也即能被 6 整除的整数。
class Solution:
def averageValue(self, nums: List[int]) -> int:
vals = [x for x in nums if x % 6 == 0]
return sum(vals) // len(vals) if vals else 0
2. 最流行的视频创作者

这是一道「语文题」,比较绕,要仔细读懂要计算的是啥。
class Solution:
def mostPopularCreator(self, creators: List[str], ids: List[str], views: List[int]) -> List[List[str]]:
# 统计每个创作者的流行度
cp = {}
for c, v in zip(creators, views):
cp[c] = cp.get(c, 0) + v
# 最大流行度
most_c = max(cp.values())
# 统计每个最流行创作者的最流行的作品
cv = {}
for c, i, v in zip(creators, ids, views):
if cp[c] == most_c:
cv[c] = min(cv.get(c, (1, "")), (-v, i))
return [(k, v[1]) for k, v in cv.items()]
3. 美丽整数的最小增量

简而言之,很直觉性的一个猜想是,我们可能应该选取 x 直到某个数位(比如十位,百位)恰好发生进位,此时能够显著减小数位和。
不难证明这一猜想的正确性。在 10 位上 (x < 10) 显然是成立的。在百位位上,如果 x 没有令百位发生进位,这个 x 一定劣于十位进位方案。如此递推即可证明。
class Solution:
def makeIntegerBeautiful(self, n: int, target: int) -> int:
# mask 是当前要处理的数位的标记
res, mask = 0, 1
while sum(int(c) for c in str(n)) > target:
# 从十位开始处理,每次循环右移一个数位
mask *= 10
tail = n % mask
# 取补
res += mask - tail
n += mask - tail
return res
4. 移除子树后的二叉树高度
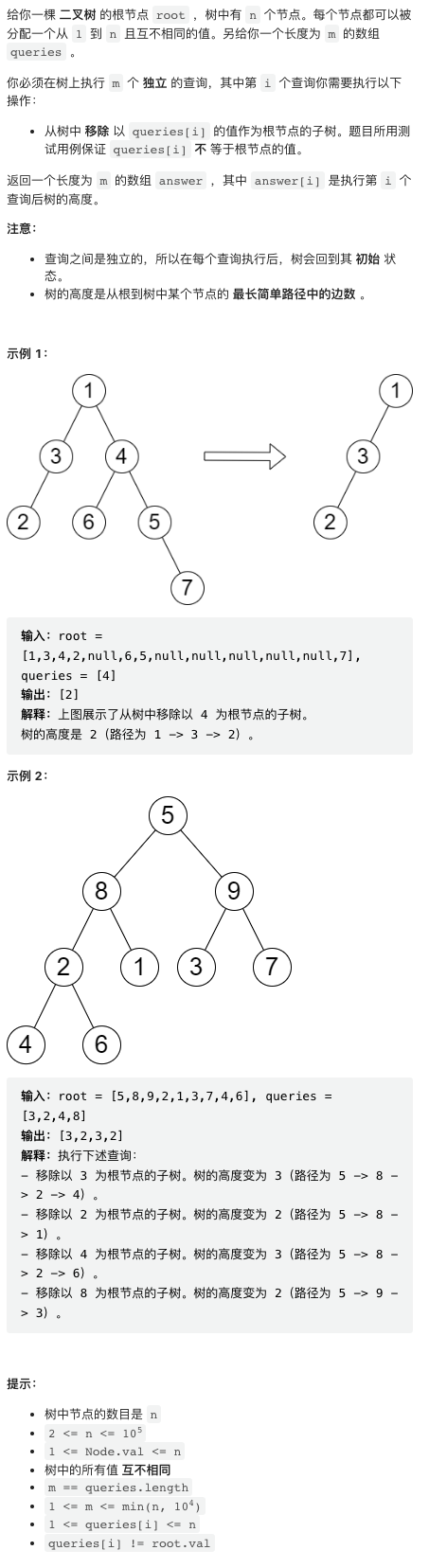
问题很简单,删除二叉树某个子树之后,求剩下的二叉树高度。这个题目的思路稍微有点反常规。考虑删除的子树节点所在的层,如果这一层高度最高的子树没有被删除,则原二叉树高度不变。否则,剩余的二叉树高度就等于第二高的子树高度加上这一层的深度。
class Solution:
def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
# key: 节点值
# value: 节点的高度和深度(从根节点到该节点的距离)
height, depth = defaultdict(int), defaultdict(int)
# dfs 求解高度和深度
def dfs(node, d):
if node:
depth[node.val] = d
h = max(dfs(node.left, d + 1), dfs(node.right, d + 1)) + 1
height[node.val] = h
return h
return -1
dfs(root, 0)
# key: 每一层的深度
# value: 这一层所有的节点对应的子树高度、节点值
tier = defaultdict(list)
for node in height:
tier[depth[node]].append((height[node], node))
# 把每一层所有的节点按高度排序
for t in tier.values():
t.sort()
res = []
for q in queries:
d = depth[q]
t = tier[d]
# 剩余的子树高度
# 如果这一层只有一个节点,没有剩余子树,高度记为 -1
# 否则,检查被删除的节点是不是最高子树
# 如果是,剩余子树高度为次高子树高度,否,则为最高子树高度
h = -1 if len(t) == 1 else (t[-1][0] if t[-1][1] != q else t[-2][0])
res.append(d + h)
return res