本周几道题目难度一般,最后一题并不是很难,但数据规模稍微有点大 Python 代码容易超时。
| 中国站传送门 | 国际站传送门 |
1. 公因子的数目

比较简单,逐个检查即可。Python 代码只需要一行。
class Solution:
def commonFactors(self, a: int, b: int) -> int:
return sum(1 for x in range(1, min(a, b) + 1) if a % x == 0 and b % x == 0)
2. 沙漏的最大总和
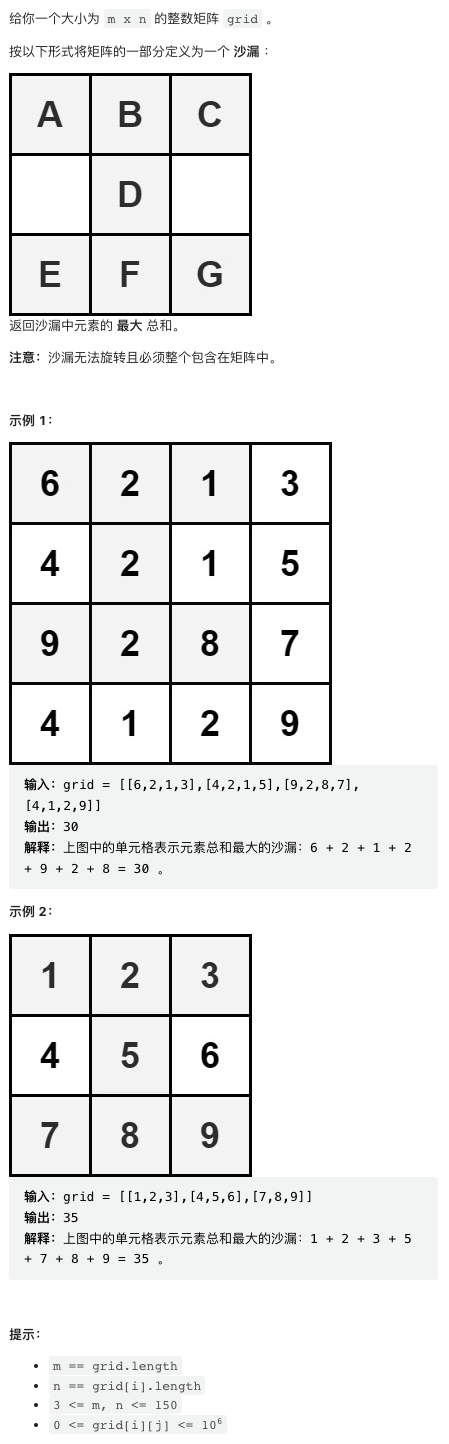
同样非常简单,遍历即可,注意不要越界。
class Solution:
def maxSum(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
res = 0
for i in range(m - 2):
for j in range(n - 2):
res = max(
res,
grid[i][j] + grid[i][j + 1] + grid[i][j + 2] +
grid[i + 1][j + 1] +
grid[i + 2][j] + grid[i + 2][j + 1] + grid[i + 2][j + 2]
)
return res
3. 最小 XOR

题目本身不困难,但实现时务必小心,这种精细操作题目比较出 BUG.
class Solution:
def minimizeXor(self, num1: int, num2: int) -> int:
def pop_count(x):
return bin(x).count('1')
c1, c2 = pop_count(num1), pop_count(num2)
if c1 >= c2:
# most significant bit
ms = 1 << (len(bin(num1)) - 3)
mask = ms
while pop_count(num1 & mask) < c2:
mask = (mask >> 1) + ms
return num1 & mask
else: # c1 < c2
mask = 1
while pop_count((~num1 & mask)) + c1 < c2:
mask = (mask << 1) + 1
return num1 | mask
4. 对字母串可执行的最大删除数

这个题目本身并不是特别困难,但题目数据规模有点大,Python 代码容易超时。
class Solution:
def deleteString(self, s: str) -> int:
n = len(s)
# lp[i][j] is longest prefix for i and j
lp = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(n - 1, -1, -1):
for j in range(i, n):
if s[i] == s[j]:
lp[i][j] = lp[i + 1][j + 1] + 1
res = [1] * n
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
if j + j - i > n:
break
if lp[i][j] >= j - i:
res[i] = max(res[i], res[j] + 1)
return res[0]