本周几道题目难度一般,最后一题比较精巧,需要使用并查集,难倒一片选手。
1. 按身高排序

非常简单的一道题目,排序输出即可。
class Solution:
def sortPeople(self, names: List[str], heights: List[int]) -> List[str]:
p = sorted(zip(heights, names), reverse=True)
return [x[1] for x in p]
2. 按位与最大的最长子数组

本题的要点在于,「按位与最大的最长子数组」就是数组中最长的连续的最大值。
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
maxVal = repeat = res = -1
for i in range(len(nums)):
if nums[i] > maxVal:
maxVal = nums[i]
res = repeat = 1
elif nums[i] == maxVal:
if i != 0 and nums[i - 1] == maxVal:
repeat += 1
else:
repeat = 1
res = max(res, repeat)
return res
3. 找到所有好下标

DP 求每个位置之前的递减字串长度和之后的递增字串长度。
class Solution:
def goodIndices(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
dec, inc = [0] * n, [0] * n
for i in range(1, n):
if i != 1 and nums[i - 1] <= nums[i - 2]:
dec[i] = dec[i - 1] + 1
else:
dec[i] = 1
for i in range(n - 2, -1, -1):
if i != n - 2 and nums[i + 1] <= nums[i + 2]:
inc[i] = inc[i + 1] + 1
else:
inc[i] = 1
return [i for i in range(n) if inc[i] >= k and dec[i] >= k]
4. 好路径的数目
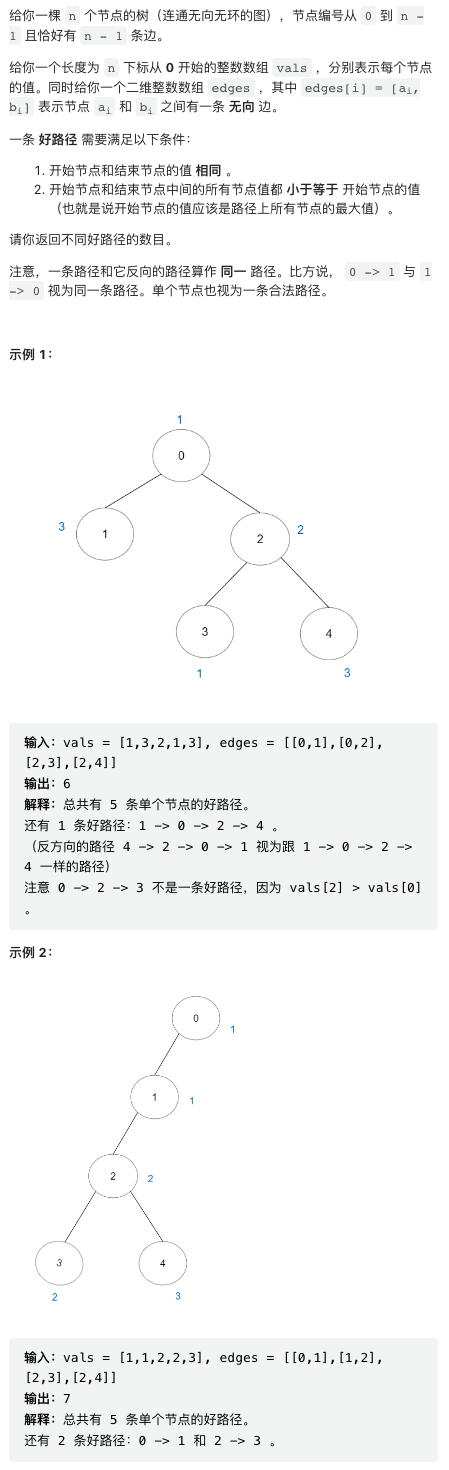

这个题目稍有难度。
首先要注意,本题的数据规模非常大。节点两两之间都有路径,因此好的路径数目最多可以达到 O(n^2) 量级,本题的数据规模高达 n = 3 * 10 ^ 4, 因此所有「逐一验证」(也就是一个一个数)的方法都会超时,必须给出一个复杂度低于 O(n^2) 的解法。
一个很有启发性的点是,对于 vals 都等于最大值最大的一组节点,它们两两之间的路径都必然是好路径。进一步思考,一个自然的思路就是,考虑一组 vals 相等(等于 x)的节点,先只考虑两个端点都小于等于 x 的边构成的子图,在这个子图上彼此连通的点之间的路径,都是好路径。
基于这个思路,使用一系列「小技巧」,并使用并查集,能够把时间复杂度控制在接近 O(n log n).
class Solution:
def numberOfGoodPaths(self, vals: List[int], edges: List[List[int]]) -> int:
n = len(vals)
pvals = sorted([(x, i) for i, x in enumerate(vals)])
we = sorted([(max(vals[x], vals[y]), x, y) for x, y in edges])
mfs = list(range(n))
def find(x):
if mfs[x] == x:
return x
mfs[x] = find(mfs[x])
return mfs[x]
def merge(x, y):
mfs[find(y)] = find(x)
gcnt = [0] * n
res = 0
i = j = p = q = 0
while(i < n):
limit = pvals[i][0]
while(j < n and pvals[j][0] == limit):
j += 1
while(q < n - 1 and we[q][0] <= limit):
q += 1
for k in range(p, q):
merge(we[k][1], we[k][2])
for k in range(i, j):
gcnt[find(pvals[k][1])] += 1
for k in range(i, j):
g = find(pvals[k][1])
gc = gcnt[g]
gcnt[g] = 0
res += gc * (gc + 1) // 2
i, p = j, q
return res
class Solution {
struct MergeFindSet {
std::vector<int> p;
MergeFindSet(int n) : p(n) { init(); }
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
void merge(int root, int child) { p[find(child)] = find(root); }
void init() {
for (int i = 0; i < int(p.size()); i++) p[i] = i;
}
};
public:
int numberOfGoodPaths(vector<int>& vals, vector<vector<int>>& edges) {
int n = vals.size();
vector<pair<int, int>> pvals;
for(int i = 0; i < n; i++) {
pvals.push_back({vals[i], i});
}
sort(pvals.begin(), pvals.end());
vector<tuple<int, int, int>> we;
for(int i = 0; i < n - 1; i++) {
int x = edges[i][0], y = edges[i][1];
we.push_back({max(vals[x], vals[y]), x, y});
}
sort(we.begin(), we.end());
vector<int> gcnt(n);
MergeFindSet mfs(n);
int res = 0;
for(int i = 0, j = 0, p = 0, q = 0; i < n; p = q, i = j) {
int limit = pvals[i].first;
while(j < n and pvals[j].first == limit) j++;
while(q < n - 1 and get<0>(we[q]) <= limit) q++;
for(int k = p; k < q; k++) {
mfs.merge(get<1>(we[k]), get<2>(we[k]));
}
for(int k = i; k < j; k++) {
int g = mfs.find(pvals[k].second);
gcnt[g]++;
}
for(int k = i; k < j; k++) {
int g = mfs.find(pvals[k].second);
int gc = gcnt[g];
gcnt[g] = 0;
res += gc * (gc + 1) / 2;
}
}
return res;
}
};