1. 和相等的子数组

暴力枚举即可。
class Solution:
def findSubarrays(self, nums: List[int]) -> bool:
sums = set()
for i in range(len(nums) - 1):
s = nums[i] + nums[i + 1]
if s in sums:
return True
sums.add(s)
return False
2. 严格回文的数字

本题也是暴力枚举。要验证 n base x 是不是回文数,求出各个数位并验证即可。
class Solution {
public:
bool isStrictlyPalindromic(int n) {
// 逐个暴力验证
for(int base = 2; base <= n - 2; base++) {
if(not pali(n, base)) return false;
}
return true;
}
vector<int> nums;
bool pali(long long n, long long base) {
nums.clear();
// 求出各个数位
while(n) {
nums.push_back(n % base);
n /= base;
}
// 验证回文数
for(int i = 0, j = int(nums.size()) - 1; i <= j; i++, j--) {
if(nums[i] != nums[j]) return false;
}
return true;
}
};
这个版本是最容易理解、最容易实现的版本。但本实现中的 pali 函数,还有一种空间复杂度是 O(1) 的实现。这在比赛中其实没什么大用处,但可以应付面试官。
bool pali(long long n, long long base) {
// 将 left, right 分别指向 n 的最高、最低有效位 1 代表的数值
long long left = 1, right = 1;
while(left * base <= n) left *= base;
// 然后,对称移动双指针,检查对应位置是否相等
while(left > right) {
// n / right % base 就是 n 在 right 对应的位置的数字
if(n / right % base != n / left % base) return false;
left /= base, right *= base;
}
return true;
}
有种直觉,这题目的条件非常苛刻,并且给出的例子都是 false. 有理由怀疑,并不存在满足要求的数。可以暴力枚举验证,确实不存在这样的数。因此本题最简单的代码是,
class Solution {
bool isStrictlyPalindromic(int n) {
return false;
}
}
这也不难证明。 n = 4 已经有验证不满足。当 n >= 5 时,总会有 n = 12 (base n - 2). 所以所有的数都不满足要求。
3. 被列覆盖的最多行数
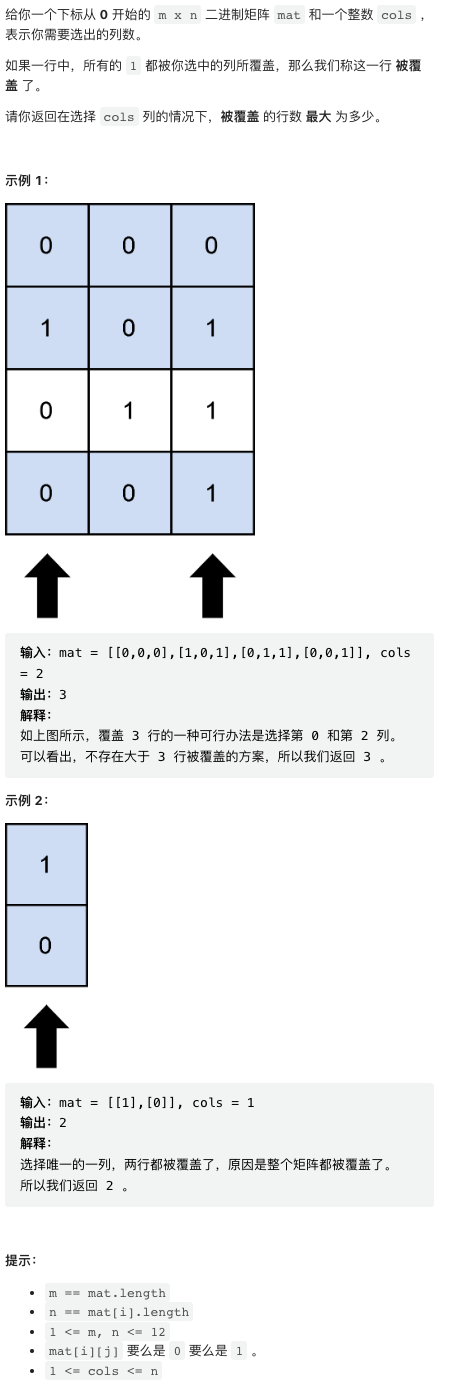
本题是 bit mask 暴力枚举,这周题目有太多暴力枚举。由于数据规模较小,借助 bit mask 暴力枚举所有可能的 cols 组合并一一验证即可。
class Solution {
public:
int maximumRows(vector<vector<int>>& mat, int cols) {
int m = mat.size(), n = mat[0].size(), res = 0;
// mask 每一个比特位代表一列是否被选中
for(unsigned mask = 1; mask <= (1 << n) - 1; mask++) {
// 这是一个 G++ 编译器内置函数,可以求指定数字的二进制表示中有多少 1
// 这个函数并不总是可用,提交前记得先试一下
if(__builtin_popcount(mask) != cols) continue;
// 计数有多少行满足条件
int cnt = 0;
for(int i = 0; i < m; i++) {
bool cover = true;
// 检查某一行是否满足条件
for(int j = 0; j < n and cover; j++) {
if(mat[i][j] and not (mask & (1 << j))) cover = false;
}
cnt += cover;
}
// 更新最大满足条件的行数
res = max(res, cnt);
}
return res;
}
};
4. 预算内的最多机器人数目

最近好多滑动窗口。。
本题使用滑动窗口的前提是,尽管总开销的计算公式比较复杂,但它是单调递增的,并且加入、减去一个元素的更新计算都不困难。滑动窗口计算 sum(runningCosts) 很容易,计算 max(chargeTimes) 稍微复杂一点。如果不记得双端队列滑动窗口最大值写法了,可以用 multiset 应付一下。
class Solution {
public:
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget) {
// 窗口中所有 chargeTimes, multiset 可以快速求最大值
multiset<int> mwin;
// 窗口中总 cost
long long cost = 0;
// left: 窗口 left 指针
int res = 0, left = 0, n = chargeTimes.size();
for(int i = 0; i < n; i++) {
// 将 i 加入窗口
mwin.insert(chargeTimes[i]);
cost += runningCosts[i];
// 左侧元素移出窗口,直到满足条件
while(left <= i and *mwin.rbegin() + (i - left + 1) * cost > budget) {
mwin.erase(mwin.find(chargeTimes[left]));
cost -= runningCosts[left];
left++;
}
res = max(res, i - left + 1);
}
return res;
}
};
这道题目比较漂亮的写法是使用双端队列求滑动窗最大值,双端队列比 multiset 效率更高。
双端队列求滑动窗最大值这个算法在 leetcode 比较常见。以本题为例,队列中保持元素单调递减,并从左侧 pop 需要出队的元素。这样一来,就能保证最左侧元素一直都是窗口中最大元素。
class Solution {
public:
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget) {
int n = chargeTimes.size();
// 单调递减队列,用于求解窗口最大值
deque<int> mwin;
// 窗口中总 cost
long long cost = 0;
int res = 0, left = 0;
for(int i = 0; i < n; i++) {
// 将队列右侧比当前元素小的元素全部 pop
while(mwin.size() and chargeTimes[mwin.back()] < chargeTimes[i]) { mwin.pop_back(); }
// 当前元素入队
mwin.push_back(i);
// 更新 cost
cost += runningCosts[i];
// pop 左侧元素,直到满足 budget 要求
while(left <= i and chargeTimes[mwin[0]] + (i - left + 1) * cost > budget) {
left++;
// 从队列中 pop 左侧元素
if(mwin.size() and mwin[0] < left) mwin.pop_front();
// 更新 cost
cost -= runningCosts[left - 1];
}
res = max(res, i - left + 1);
}
return res;
}
};