朴素贝叶斯模型直接从数据中统计 $P(y), P(x \mid y)$ 进而计算 $P(x,y)$,属于生成模型。$P(y), P(x \mid y)$ 都是多项分布。
既然可以统计 $P(y), P(x \mid y)$,那为什么不直接统计 $P(x,y)$ ?这是因为对于分类问题数据集 ${(x_n, y_n)}$,数据相对于 $x,y$ 可能取值数目充足时,可以直接使用频数估计频率统计得到后验分布 $P(x,y) = \hat P(x,y)$。然而,对于取值较为复杂的数据,当 $x_n, y$ 有 $K_n, L$ 种取值时,$P(x,y)$ 共有 $L \prod K_n$ 种取值,直接从数据中统计这些值作为模型参数对于高维数据会面临参数过多和数据不足的情况。
朴素贝叶斯假设:
\[P(x_1, x_2, \cdots x_N \mid y) = \prod_i P(x_n \mid y)\]这样模型参数 $P(y), P(x \mid y)$ 参数数目下降到 $L + L \sum K_n$,从数据中学习模型参数成为可能。即便如此,朴素贝叶斯只适用于 $x_n$ 离散、有限取值且取值较少的情况,否则需要预先对数据进行分桶。
【模型参数】:$P(y), P(x \mid y)$ 【模型预测方式,后验概率最大化】:$y = \arg\max_y P(y \mid x) = \arg\max_y P(y) \prod_n P(x_n \mid y)$
模型参数极大似然估计
没有先验假设的估计:
\[\begin{align*} P(y = y_k) &= \frac{C(y=y_k)}{D} \\ P(x_n = a_{n,k} \mid y_k) &= \frac{C(x_n = a_{n,k}, y=y_k)}{C(y=y_k)} \end{align*}\]上式中 $C(y=y_k)$ 表示计数满足 $y=y_k$ 的样本数量,$D$ 为数据集大小。
下面以 $P(y=y_k)$ 为例进行推导,记 $p_k = P(y=y_k)$.
\[\begin{align*} p_1,\cdots,p_K &= \arg\max_{p_1,\cdots,p_K} P(X, Y \mid p_k) \\ &= \arg\max_{p_1,\cdots,p_K} \prod_n\left[P(y_n)\prod_i P(x^{(i)}_n \mid y_n)\right] \\ &= \arg\max_{p_1,\cdots,p_K} \prod_n P(y_n) \\ &= \arg\max_{p_1,\cdots,p_K} \prod_k p_k^{C(y=y_k)} \\ \end{align*}\]$C$ 表示计数样本中 $y=y_k$ 出现的次数,记 $C_k = C(y=y_k)$。于是问题转换为等式约束下的函数极值问题:
\[\newcommand{\ps}{p_1,\cdots,p_K} \arg\min_{\ps} \left[ - \prod_k p_k^{C_k} \right] \\ \text{s.t. } \sum_k p_k = 1\]简化问题,对优化目标函数取对数:
\[\newcommand{\ps}{p_1,\cdots,p_K} \arg\min_{\ps} \left[ - \sum_k C_k \log p_k \right] \\ \text{s.t. } \sum_k p_k = 1\]使用拉格朗日乘子法时,引入乘子 $D$,构建拉格朗日函数:
\[L = \left[ - \sum_k C_k \log p_k \right] + D\left(\sum_k p_k - 1\right)\]引入拉格朗日乘子项之后,上式求偏导时可以认为 $p_k$ 之间不再存在约束关系,因此 $\frac{\partial p_k}{\partial p_j} = \delta(k,j)$. 于是:
\[\frac{\partial}{\partial p_k} L = - \frac{C_k}{p_k} + D = 0 \\ p_k = \frac{C_k}{D}\]利用 $\sum_k p_k = 1$ 可的 $D = \sum_j C_j$,于是:
\[p_k = \frac{C_k}{\sum_j C_j}\]贝叶斯估计
引入了平滑项:
\[P(y = y_k) = \frac{\lambda + C(y=y_k)}{K\lambda + D} \\ P(x_n = a_{n,k} \mid y_k) = \frac{\lambda + C(x_n = a_{n,k}, y=y_k)}{K_n\lambda + C(y=y_k)}\]下面给出推导。先验信息的似然函数是一个多项分布: $Mult(\vec{n}\mid\vec{p},N)$
\[P(Y|\theta) = \prod_{k=1}^{K}\prod_{i=1}^{N}P(y_i=c_k)^{I(y_i=c_k)}\\ = \prod_{k=1}^{K} P(y_i=c_k)^{\Sigma_{i=1}^{N}I(y_i=c_k)}\\ = \prod_{k=1}^{K}P_k^{n_k}\]故共轭先验分布采用Dirichlet 分布: $Dir(\vec{P}\mid\vec{\alpha})$
\[P(\theta) = \frac{\Gamma(\Sigma_{k=1}^{K}\alpha_k)}{\prod_{k=1}^{K}\Gamma(\alpha_k)} \prod_{k=1}^{K}P_k^{\alpha_k} = \frac{\prod_{k=1}^{K}P_k^{\alpha_k}}{\Delta(\vec{\alpha})}\]后验分布仍然是Dirichlet分布,
\[\frac{ Mult(\vec{n}|\vec{p},N) Dir(\vec{P}|\vec{\alpha}) }{ \int Mult(\vec{n}|\vec{p},N) Dir(\vec{P}|\vec{\alpha}) } = \frac{ \prod_{k=1}^{K} P_k^{n_k+\alpha_k} }{ \int \prod_{k=1}^{K} P_k^{n_k+\alpha_k}d\vec{P} } = \frac{ \prod_{k=1}^{K} P_k^{n_k+\alpha_k} }{ \Delta(\vec{\alpha}+\vec{n}) } \\\]所以后验分布的参数为
\[\Big( \frac{n_1+\alpha_1}{\Sigma_{k=1}^{K}(n_k+\alpha_k)}, \cdots, \frac{n_K+\alpha_K}{\Sigma_{k=1}^{K}(n_k+\alpha_k)} \Big)\]进一步简化
\[\Big( \frac{\Sigma_{i=1}^{N}I(y_i=c_k)+\alpha_1}{N+\Sigma_{k=1}^{K}\alpha_k}, \cdots, \frac{\Sigma_{i=1}^{N}I(y_i=c_K)+\alpha_K}{N+\Sigma_{k=1}^{K}\alpha_k} \Big)\]如果我们取先验信息为$\alpha_1=\alpha_2=\cdots=\alpha_K = \lambda \quad (\lambda>0)$, 则先验概率的贝叶斯估计为
\[\Big( \frac{\Sigma_{i=1}^{N}I(y_i=c_k)+\lambda}{N+K\lambda}, \cdots, \frac{\Sigma_{i=1}^{N}I(y_i=c_K)+\lambda}{N+K\lambda} \Big)\]同理条件概率的似然函数为
\[P(X^{(j)}|Y=c_k) = \prod_{j=1}^{S_j} P(x_i^{(j)}=a_{ji}|y_i=c_k)^{\Sigma_{i=1}^{N} I(x_i^{(j)}=a_{ji},y_i=c_k)} \\ = \prod_{j=1}^{S_j}P_j^{m_j}\]取先验分布 $Dir(\vec{p}\mid\vec{\beta})$, 故后验分布为为$Dir(\vec{p}\mid\vec {\beta}+\vec{m})$,其参数为
\[\Big( \frac{\Sigma_{i=1}^{N}I(x_i^{(j)}=a_{ji},y_i=c_k)+\beta_1} {\Sigma_{i=1}^{N} I(y_i=c_k)+\Sigma_{j=1}^{Sj}\beta_j}, \cdots, \frac{\Sigma_{i=1}^{N}I(x_i^{(j)}=a_{ji},y_i=c_k)+\beta_{S_j}} {\Sigma_{i=1}^{N} I(y_i=c_k)+\Sigma_{j=1}^{Sj}\beta_j}, \Big)\]如果我们取先验信息为$\beta_1=\beta_2=\cdots=\beta_K = \lambda \quad (\lambda>0)$, 则条件概率的贝叶斯估计为
\[\Big( \frac{\Sigma_{i=1}^{N}I(x_i^{(j)}=a_{ji},y_i=c_k)+\lambda} {\Sigma_{i=1}^{N} I(y_i=c_k)+S_j \lambda}, \cdots, \frac{\Sigma_{i=1}^{N}I(x_i^{(j)}=a_{ji},y_i=c_k)+\lambda} {\Sigma_{i=1}^{N} I(y_i=c_k)+S_j \lambda} \Big)\]以下是一些不成熟的思考,复习时可以跳过。
使用贝叶斯估计策略的关键问题在于确定模型参数 $p_k$ 的先验分布,课本上并没有给出先验分布。结合拉格朗日乘子法求解步骤,在这里尝试从该平滑项逆推先验分布。
最大似然估计结果:
\[p_k = \frac{C_k}{\sum_k C_k}\]贝叶斯估计结果:
\[p_k = \frac{C_k + \lambda}{\sum_k(C_k + \lambda)}\]对比两式,结合最大似然估计的拉格朗日函数,逆推贝叶斯估计的最优化问题的拉格朗日函数:
\[\frac{\partial}{\partial p_k} L = - \left( \frac{C_k}{p_k} + \frac{\lambda}{p_k} \right) + D \\ L = - \left[ \lambda \log p_k \sum_k C_k \log p_k \right] + D\left(\sum_k p_k - 1\right) \\\]该拉格朗日函数对应的优化问题可能是:
\[p_k = \arg\max p_k^\lambda \prod_k p_k^{C_k}\]于是,不考虑归一项,$p_k$ 先验分布取 $p_k^\lambda$。这不是合理的概率分布,先验概率分布没有理由是 $p_k$ 越大概率越大。
但是,考虑二分类问题,可以定义分布 $P’(p_0) = p_0^\lambda(1-p_0)^\lambda$. 这是一个合理的分布,当 $\lambda = 0$ 时退化为均匀分布,当 $\lambda = 1$ 时分布为:
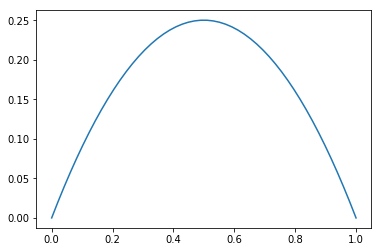
当 $\lambda$ 越大,该分布越「尖锐」,代表先验有更高的信心假设 $y$ 分布是均匀分布。当 $\lambda = \infty$ 时 $p_0’=0.5$ 代表先验完全确定 $y$ 分布是均匀分布。这些结论都是合理的。
于是有一个新问题:$P(p_0)=p_0^\lambda$ 和 $P’(p_0) = p_0^\lambda(1-p_0)^\lambda$ 这两个分布是什么关系?仔细考虑,在 $p_0 + p_1 = 1$ 的约束下,$p_0,p_1$ 不是两个独立的随机变量,联合概率分布 $P(p_0,p_1)$ 是没有意义的。但是,我们可以定义一个伪联合概率分布 $P’(p_0,p_1)$,这是一个二元函数,然后可以认为该函数在 $p_0 + p_1 = 1$ 的超平面上的「截面函数」就是真实的 $P(p_0)$ 或 $P(p_1)$ 概率分布。
本题目中,逆推得到的 $P(p_k)$ 分布就是这样一个伪联合概率分布的边缘分布。利用约束关系消元,将伪联合概率分布限制到超平面上,就能得到真正的概率分布。
贝叶斯估计的最初形式应该是:
\[p_1, \cdots, p_{K-1} = \arg\max_{p_1, \cdots, p_{K-1}} P( Y \mid p_1,\cdots, p_{K-1}) P(p_1, \cdots, p_{K-1}) \\\]注意,$K$ 分类问题的 $P(y=y_k)$ 参数只有 $K-1$ 个,因为有约束关系 $\sum_k p_k = 1$. 但是,可以引入辅助变量 $p_K$,将问题表述为:
\[p_1, \cdots, p_K = \arg\max_{p_1, \cdots, p_K} P( Y \mid p_1,\cdots, p_K) P(p_1, \cdots, p_K)\]而约束关系体现到先验概率分布中:
\[P(p_1, \cdots, p_k) = \left\{ \begin{array}{llr}\prod_k p_k^\lambda & \text{if} & \sum_k{p_k}=1 \\ 0 & \text{others.}\end{array} \right.\\\]约束最优问题整理为:
\[p_1, \cdots, p_K = \arg\max_{p_1, \cdots, p_K} P( Y \mid p_1,\cdots, p_K) \prod_k p_k^\lambda \\ P( Y \mid p_1,\cdots, p_K) = \prod_k p_k^{C_k} \\ \text{s.t. } \sum_k {p_k} = 1\]该问题的求解与最大似然估计约束最优化问题求解基本一致。